5. MORTALITÉS

5.1 Introduction
5.2 Estimation de la mortalité totale
5.3 Mortalité par pêche
5.4 Mortalité naturelle et allure de la croissance
5.5 Méthodes graphiques spéciales
5.6 Exercices

5.1 Introduction

L'étude des mortalités fait intervenir les taux de variation, et il est généralement plus pratique d'utiliser les taux instantanés de variation (voir sect. 2.1). En d'autres termes, la rapidité à laquelle l'effectif de la population décroît peut être exprimée par l'égalité:

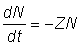
où Z est défini comme le coefficient instantané de mortalité totale. A partir de cette équation, le nombre d'animaux en vie à une époque donnée (N_t) sera donné par la formule (voir section 2.4.1, exercice 18):

N_t = N₀ e^-Zt

où N₀ = nombre en vie au temps 0.

On désire souvent étudier séparément deux causes de diminution de l'effectif de la population: morts naturelles (maladies, prédation, etc.) et captures. On peut alors écrire:

où M = coefficient de mortalité naturelle

où F = coefficient de mortalité par pêche.

Pour un intervalle très bref de temps dt, les morts provoquées par la pêche seront égales à FNdt, les morts naturelles à MNdt, et les morts totales à ZNdt. Par conséquent:

F + M = Z

autrement dit, les coefficients instantanés de mortalité s'ajoutent.

5.2 Estimation de la mortalité totale

Avant d'estimer séparément la mortalité par pêche et la mortalité naturelle, il est commode d'évaluer la mortalité totale. On peut le faire aisément si l'on connaît les abondances - par exemple N₀ et N₁ - de tout groupe d'animaux aquatiques à deux moments donnés, car alors la fraction survivante est 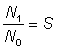, et le coefficient de mortalité totale est donné par la formule:

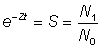, (5.1)

ou encore:

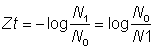
où t = intervalle de temps

Il existe un cas particulier évident quand t = un an. Ces formules demeurent valables quand on ignore les abondances réelles mais dispose d'indices, par exemple prises par unité d'effort, autrement dit de nombres n₀ et n₁ proportionnels à N₀ et à N₁. On a alors:

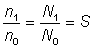
Souvent, abondances ou indices d'abondance ne sont pas connus à un moment précis, mais seulement en tant que moyennes de périodes limitées (par exemple un an). L'abondance moyenne durant la période de durée T, exprimée en fonction de l'abondance N au début de la période et du coefficient Z de mortalité totale, peut être indiquée 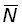; le nombre d'animaux en vie au temps t est égal à Ne^-Zt, de sorte que:

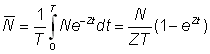
En désignant par des indices appropriés les valeurs des abondances et des mortalités durant les périodes 0 et 1 (espacées d'un an), de durée T, on a:

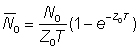
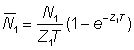
ainsi que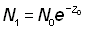

Faisons le rapport des abondances moyennes:

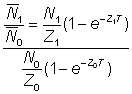
c'est-à-dire 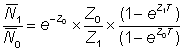, (5.2)

Lorsque Z₀ = Z₁ = Z, l'équation 5.2 se réduit à:

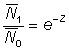ou: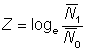

c'est-à-dire que le rapport des abondances moyennes peut être utilisé de la même manière que le rapport des abondances instantanées dans l'équation 5.1.

On peut également faire la simplification si Z₀T et Z₁T sont tous deux petits, même s'ils sont inégaux, car alors 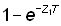est presque égal à Z₁T, et il en va de même pour 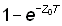. Les deux derniers facteurs de l'équation 5.2 s'annulent, et celle-ci devient: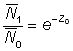

Le rapport des abondances moyennes durant deux périodes fournit donc une bonne estimation des survivants pendant l'année, que la mortalité soit constante ou que le changement subi par l'effectif durant ces deux périodes soit faible. Même si ces conditions ne sont pas remplies, le rapport peut encore donner une première approximation assez satisfaisante, sous réserve de corrections que l'on peut déduire de l'équation 5.2.

Les formules ci-dessus seront habituellement appliquées aux abondances de classes d'âges individuelles, et permettront d'estimer les mortalités entre n'importe quelle paire d'années consécutives et pour n'importe quelle classe d'âge pleinement recrutée. Ces estimations seront probablement très nombreuses, et il faudra décider quelle est la meilleure pouvant être obtenue par combinaison. Une seule estimation combinée n'est valable que s'il n'y a pas de différences systématiques dans la mortalité, en fonction de l'âge ou en fonction du temps, au cours de la période considérée; ces différences peuvent être très facilement décelées à l'aide d'une table comme la table 5.1 ci-après, soit par examen des moyennes de rangées et des colonnes, soit, de façon plus rigoureuse, par une épreuve statistique - analyse de la variance par exemple.

TABLE 5.1. - EXEMPLE HYPOTHÉTIQUE D'ESTIMATIONS DE COEFFICIENTS INSTANTANÉS DE MORTALITÉ TOTALE POUR DIFFÉRENTES PAIRES D'ANNÉES ET DE GROUPES D'AGE

	Age
Années	4/5	5/6	6/7	7/8	8/9	9+/10+	Moyenne
1950/51	0,75	0,80	0,65	0,70	0,55	0,75	0,70
1951/52	0,70	0,80	0,75	0,60	0,65	0,55	0,68
1952/53	0,65	0,60	0,85	0,70	0,85	0,70	0,72
1953/54	0,70	0,75	0,65	0,90	0,50	0,50	0,67
Moyenne	0,70	0,74	0,72	0,72	0,64	0,62	0,69

Dans une table de ce genre, les éléments doivent toujours être des coefficients instantanés et non des pourcentages de mortalité. En effet, on démontre aisément que ces derniers sont biaises - sous-estimés d'une quantité moyenne dépendant de la variance des données - l'erreur systématique pouvant être très marquée lorsqu'on prend la moyenne de plusieurs estimations. Ce biais provient de ce que le numérateur de l'équation 5.1 n'est pas connu exactement: celui-ci s'écartant de la valeur réelle en plus ou en moins, la sous-estimation de la fraction survivante dans le premier cas est moins importante que la surestimation dans le second, à écart égal. On obtient un biais analogue lorsqu'on compare la moyenne des inverses d'un ensemble de nombres: elle n'est pas la même que l'inverse de leur moyenne.

S'il n'y a pas de différences systématiques appréciables entre les années ou les âges, les termes de la table 5.1 peuvent être tenus comme des estimations séparées de la même mortalité réelle, et l'estimation combinée ayant la moindre variance sera obtenue en prenant la moyenne pondérée (facteurs de pondération inversement proportionnels aux variances des diverses estimations). Ces variances seront généralement inconnues, et quoique, évidemment, la variance de groupes d'âge très âgés et peu abondants soit élevée, les renseignements disponibles (données limitées sur la plie, le hareng et l'églefin) font penser qu'elle est à peu près constante pour tous les groupes d'âge bien représentés (de 4 à 11 ans pour la plie de la mer du Nord). Ainsi, si l'on combine les données pour les groupes plus âgés (par exemple dernière colonne de la table 5.1), toutes les variances seront sensiblement égales, et l'estimation d'ensemble appropriée sera fournie par la simple moyenne de toutes les estimations individuelles. L'estimation moyenne de la mortalité entre n'importe quelle paire de groupes d'âge durant toutes les années peut être déterminée de la même manière, c'est-à-dire en prenant la moyenne simple des estimations de Z pour chaque couple d'années, ou en pondérant la moyenne, accordant une valeur plus grande aux années pour lesquelles la variance de Z est probablement faible (autrement dit celles durant lesquelles on a prélevé davantage d'échantillons). Une autre méthode courante d'estimation de la mortalité entre années successives consiste à prendre la diminution des effectifs totaux de toutes les classes d'âge pleinement exploitées - par exemple, dans la table 5.1, le rapport des 4+ aux 5+. Cela revient en fait à pondérer les estimations de la table par le nombre de poissons à chaque âge.

L'effet de l'utilisation de représentations insuffisantes de l'effort et de la prise par unité d'effort (p.u.e.) telles que cette dernière n'est pas en rapport constant avec l'abondance réelle peut être déduit de l'équation 5.1. En effet, supposons que le rapport entre p.u.e. et abondance au cours des deux années soit donné, avec une notation évidente, par:

;

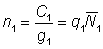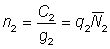
On a alors:

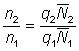
et

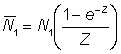
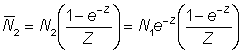
et enfin:

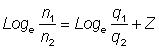, (5.3)

Ainsi, les mortalités estimées inclueront un terme supplémentaire, égal au logarithme du changement de q («disponibilité» ou «coefficient de possibilité de capture»). Une variation de q causerait, dans une présentation comme celle de la table 5.1, un changement d'année en année dans la mortalité non lié à des modifications de la pêche ou d'autres causes de mortalité.

C'est surtout lorsqu'il existe une tendance nette dans les valeurs de q que les variations de la disponibilité peuvent causer d'importantes erreurs. L'éventualité n'est peut-être guère à redouter lorsqu'on emploie des chiffres annuels, mais on est souvent tenté d'utiliser la diminution de la p.u.e. (pour un seul groupe d'âge ou pour l'ensemble du stock) durant une partie de l'année pour évaluer la mortalité. Pratiquement toutes les pêcheries accusent des modifications saisonnières plus ou moins prononcées de la p.u.e., mais alors que dans certaines ces fluctuations peuvent suivre exactement celles de l'abondance - l'accroissement provenant du recrutement et de la croissance, et la diminution uniquement de la mortalité - il arrive très fréquemment que les variations dérivent essentiellement de modifications de la «disponibilité», le poisson étant particulièrement vulnérable à la capture à certaines époques, par exemple lorsqu'il se concentre en vue du frai (on observera souvent des fluctuations analogues durant un cycle de 24 heures, cas où l'on ne saurait raisonnablement avancer que la diminution notée par exemple durant la journée provient d'une diminution de l'effectif du stock).

Par conséquent, en règle générale, il ne faut pas utiliser les modifications à court terme de la p.u.e. pour estimer les mortalités. On opérera normalement à partir de valeurs annuelles moyennes, ou de périodes espacées de 12 mois. Peut-être faudra-t-il appliquer des techniques spéciales pour estimer les indices d'abondance et, partant, les mortalités, dans les pêcheries très saisonnières, où la «pointe» de la campagne peut varier d'une année à l'autre.

Les données sur l'abondance de classes d'âge successives à un moment donné peuvent être utilisées de la même manière que celles qui ont trait à l'abondance des mêmes classes d'âge lors d'années successives. Si l'on prend t_c comme âge auquel les animaux entrent dans la phase exploitée (dans la pêcherie), moment auquel les effectifs de deux classes d'âge successives sont respectivement N₀ et N'₀, leur abondance aux âges t + 1 et t sera:

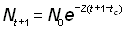
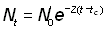
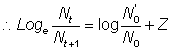, (5.4)

La p.u.e., voire des données sur les pourcentages d'âge, peuvent être utilisées directement comme indices d'abondance, car le coefficient q (relié à la disponibilité), au numérateur et au dénominateur de la fraction, se rapporte à la même période et par conséquent s'élimine. On a:

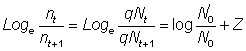, (5.5)

Les équations 5.3 et 5.5 se ressemblent beaucoup, et contiennent toutes deux un terme en plus de la mortalité vraie. Il vaut mieux employer les rapports des p.u.e. de la même classe d'âge (équation 5.3) quand la densité de la classe d'âge varie, ou lorsque les changements de la «disponibilité» sont faibles et que l'effort se mesure aisément. L'équation 5.5 convient mieux quand la mesure de l'effort est difficile ou que la classe d'âge varie peu, et aussi lorsque les données ne sont disponibles que pour des années isolées. L'un des désavantages de l'équation 5.5 est qu'elle ne mesure pas la situation présente - la mortalité additionnelle à laquelle est sujet le plus âgé des deux groupes d'âge voisins est celle qu'il subit durant sa première année dans la pêcherie, les mortalités ultérieures s'appliquant également aux deux classes. Ainsi, si un poisson entre dans la pêcherie à l'âge de 3 ans, le rapport entre poissons de 7 ans et poissons de 6 ans figurant dans les captures de 1965 donne une indication de la mortalité en 1961, année précédant immédiatement celle où le poisson maintenant âgé de 6 ans a été recruté.

Des estimations de la mortalité totale pendant une certaine période peuvent aussi être obtenues par des méthodes semi-graphiques. Si Z (mortalité totale) est constant, nous pouvons exprimer l'effectif d'une classe d'âge à n'importe quel temps t, après qu'elle ait subi la mortalité pleine et entière, par:

Nt = N₀ e^-Zt

où N₀ = nombre d'animaux au temps t = 0

Log_e N_t = Log_e N₀ - Zt

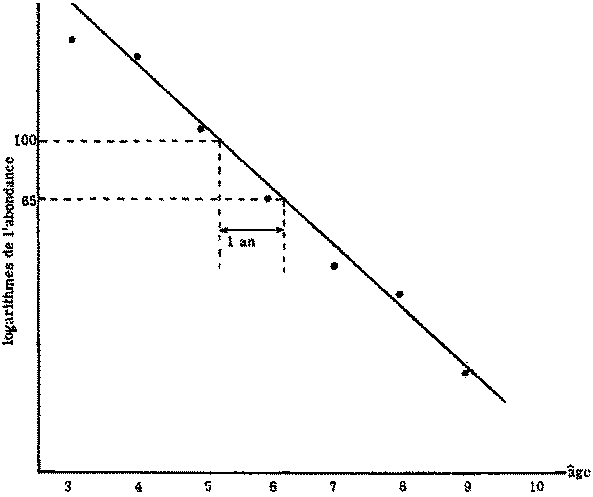
Si l'on trace Log_e Nt en fonction de t, on obtient une droite de pente - Z. Le graphique peut être établi soit pour la p.u.e., d'une seule classe d'âge à divers moments, auquel cas les déviations autres que la variance de l'échantillonnage proviendront de modifications de la «disponibilité», soit pour la densité de différentes classes d'âge au même moment - la «courbe de prise» bien connue. (Ricker, 1958, étudie en détail ce type de courbe, et fournit notamment une interprétation des courbes de prise non linéaires.) Dans le second cas, les déviations seront provoquées par des inégalités dans l'abondance initiale de la classe d'âge, mais la valeur de la «disponibilité» durant l'année de l'échantillonnage n'altérera que la position de la courbe, et non sa pente ni la dispersion des points. Cette méthode graphique peut aussi (et sans difficulté) être utilisée en traçant Nt en fonction de t sur du papier semi-logarithmique. A partir de la droite ainsi obtenue, on procédera comme suit pour estimer la mortalité: prendre sur la droite un point de valeur commode (par exemple 100), et déterminer sur la droite la valeur exactement un an plus tard (exemple 65); la fraction après un an sera alors: 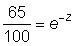, Z pouvant être obtenu immédiatement dans des tables appropriées (voir figure 5.1).

FIGURE 5.1. - Estimation de Z. Représentation graphique des logarithmes de l'abondance d'une classe d'âge en fonction de l'âge

Toutes les méthodes ci-dessus, quand elles sont appliquées à la composition par âge des prises, sont sujettes à un biais lorsque les animaux d'âges différents ne sont pas également vulnérables à l'engin utilisé. Si l'on appelle _tq et _t+1q les vulnérabilités aux âges successifs t et t + 1, les prises ou p.u.e. sont données par les expressions:

n_t = _tq · N_t

n_t+1 = _t+1q · N_t+1

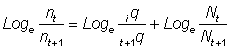
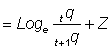
Si, dans la pratique, ce type de biais peut être difficile à déceler - sauf dans le cas de modifications soudaines liées à l'âge, auquel cas la mortalité apparente évoluera également avec l'âge - l'éventualité de son existence ne doit jamais être négligée. Du fait que cette différence de vulnérabilité selon l'âge implique que la mortalité par pêche varie avec l'âge, les formes de la répartition par âge du stock et des prises peuvent toutes deux différer beaucoup de la forme simple de la courbe de mortalité constante (voir Jones, 1964). Parfois (par exemple quand une vulnérabilité décroissante est équilibrée par une mortalité décroissante), la répartition par âge des prises peut être très proche de celle que l'on obtient pour une mortalité constante.

La mortalité totale peut aussi être estimée à partir de la «population virtuelle». La population virtuelle d'une certaine classe d'âge à son huitième anniversaire, par exemple, est le nombre total d'animaux de cette classe d'âge capturés après leur huitième anniversaire.

La mortalité durant la neuvième année de vie est alors obtenue comme étant le logarithme du rapport des populations virtuelles à 9 ans et à 8 ans. Le cas où la méthode convient probablement le mieux est celui des animaux longévifs, dont la pêche prend une grande partie mais dont la «disponibilité» est variable et difficile à mesurer (voir Fry, 1957; Bishop, 1959; Garrod, 1967).

Quand la composition par âge n'est pas connue, des estimations, parfois très bonnes, de la mortalité totale, peuvent être obtenues à partir des données relatives à la longueur. Le nombre relatif d'animaux de deux groupes de tailles différents dépendra: a) du temps mis pour passer d'une taille à l'autre; b) du taux de mortalité durant cette période; c) du temps mis pour grandir de la limite inférieure à la limite supérieure de taille de chaque classe, autrement dit la proportion d'une classe d'âge complète que représente chaque groupe de tailles. Ces facteurs admettent un cas particulièrement simple: lorsqu'il y a une série de tailles pour lesquelles la croissance est linéaire, ou à peu près. Alors, si l'abondance de chaque groupe de tailles est représentée graphiquement sur une échelle logarithmique, comme pour une courbe des prises, le graphique devrait donner une droite, de pente proportionnelle au coefficient de mortalité totale. En outre, si le taux de croissance est connu, il est possible de déterminer la valeur absolue de la mortalité. La courbe de la croissance pondérale est généralement plus linéaire pour une gamme plus étendue de tailles importantes que la courbe de la croissance en longueur. Aussi, un graphique des nombres de chaque groupe de poids en fonction du poids peut fournir une bonne estimation de la mortalité. Du point de vue mathématique, si l'on peut représenter la courbe de croissance pour une certaine gamme d'âges par la droite l_t = a + bt, et que la pente de la courbe correspondant aux nombres en fonction de la longueur soit Z', c'est-à-dire log N₁, = log N'₀ - Z'l, alors Z = bZ', ou bien, si la croissance pondérale est linéaire de sorte que W_t = C + gt, log Nw = log N₀'' - Z"W, et Z = gZ".

La mortalité totale peut également Se mesurer, dans l'hypothèse d'une situation stable, par l'âge ou la longueur moyenne dans la population exploitée, qui seront les mêmes que dans les prises si la pêche n'est pas sélective. Si âges et longueurs des animaux entrant dans la phase exploitée et moyennes dans les prises sont t_c, l_c, 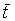et 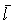, respectivement, on peut aisément en tirer les expressions suivantes pour Z (voir Beverton et Holt, 1956):

;

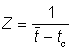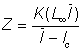
où K et L_¥ sont les constantes de l'équation de von Bertalanffy.

5.3 Mortalité par pêche

Aucune des nombreuses méthodes d'estimation de la mortalité par pêche n'est entièrement satisfaisante; dans la pratique, il est bon d'obtenir des estimations à l'aide d'autant de méthodes indépendantes que possible. On trouvera ci-après un bref exposé des principaux procédés, les plus directs venant en premier.

a) Recensement direct. Si le stock total est connu, la mortalité par pêche peut être calculée immédiatement à partir de la prise. Les chiffres totaux peuvent être obtenus par un dénombrement complet ou par un sondage - par exemple saumons remontant un cours d'eau, ou baleines aperçues dans une aire connue. Généralement, la seule méthode praticable pour les poissons marins est le recensement des femelles adultes par comptage du nombre d'œufs pondus, après récolte de plancton. On estime alors le nombre total d'après la proportion de femelles adultes dans les prises et leur fécondité. Cette méthode offre l'avantage de se prêter mieux que la plupart des autres à la détermination du degré de confiance statistique des estimations, quoique celui-ci puisse passablement varier (voir English, 1964).

b) Aire balayée. De la définition du coefficient instantané de mortalité, il ressort que la mortalité par pêche provoquée par une seule opération - que l'on peut considérer comme le fait de prendre une part infiniment petite du stock total - est égale à la fraction de la population qui est capturée. Si le stock est uniformément réparti et si l'engin prend effectivement tous les animaux situés à l'intérieur d'une aire a, l'aire totale habitée par le stock étant A, le coefficient de mortalité par pêche est égal à 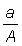. La mortalité par pêche durant un temps D t pour l'ensemble de la pêcherie (FD t) est alors 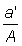, a' étant la A somme des aires couvertes par tous les navires de la flotte.

Cette méthode est évidemment limitée aux engins pour lesquels la superficie couverte peut être aisément estimée: pour un trait de chalut, par exemple, ce sera le produit de la distance entre panneaux et de la distance parcourue. Il existe deux grandes causes d'erreurs, agissant en sens inverse. Premièrement, comme certains des animaux se trouvant dans l'aire balayée par l'engin peuvent s'échapper, on risque de surestimer la mortalité. Deuxièmement, comme il a été dit dans la section consacrée à l'effort de pêche, la densité des animaux dans la zone pêchée est supérieure à la densité moyenne, d'où une sous-estimation de la mortalité par pêche. La méthode ne peut donc fournir une estimation exacte de la mortalité par pêche, mais donne parfois d'utiles indications de l'ordre de grandeur de celle-ci. En particulier, elle est souvent précieuse en ce qu'elle révèle si la pêche est susceptible d'exercer un effet appréciable. La méthode peut également servir lorsque l'aire occupée par les animaux peut être déterminée par sondage aux ultrasons. (Pour l'emploi des écho-sondeurs et autres appareils pour mesurer l'abondance, et, partant, la mortalité par pêche, voir les actes du Colloque CIEM sur la mesure de l'abondance du poisson, notamment les communications de Cushing et de Federov, et le rapport du Groupe de travail du Comité consultatif de la recherche sur les ressources de la mer (CCRRM) sur l'estimation directe et accélérée de l'abondance du poisson.)

c) Marquage. Le marquage constitue bien entendu l'une des méthodes les plus connues pour apprécier la mortalité par pêche. Si la population des poissons marqués est à tous égards identique au stock total, la mortalité par pêche et la mortalité totale sont aisément déterminées à partir du nombre de poissons marqués recapturés. Les diverses façons de procéder sont étudiées au chapitre suivant.

d) Changements dans la mortalité totale. Toute modification de l'intensité de pêche agit sur la mortalité par pêche, et donc aussi sur la mortalité totale. Si l'on peut établir une relation quantitative entre l'évolution de cette dernière et les modifications connues de l'effort de pêche, il sera possible de déduire une valeur du coefficient de mortalité par pêche pour tout niveau donné d'effort. Pour un temps T, on peut écrire:

ZT = (F + M) T = qf + MT

où/est l'effort total durant la période.

Si T = 1, on peut écrire, à partir des données sur l'effort durant 1 an:

Z = F + M = qf + M, (5.6)

ou encore, en fonction de l'intensité de pêche :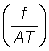

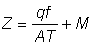
Si l'on connaît une série de paires de valeurs correspondantes de f (effort de pêche) et de Z (coefficient de mortalité totale), l'équation 5.6 fournit entre ces valeurs une relation linéaire. Pour deux paires de valeurs, on peut obtenir q et M par un système de deux équations du premier degré à deux inconnues. Pour un plus grand nombre de valeurs, en portant sur un graphique Z en fonction de f, on obtient en principe une ligne droite, de pente q, qui coupe l'axe des y au point M (voir figure 5.2).

FIGURE 5.2. - Estimation de F et de M. Représentation graphique du coefficient de mortalité totale en fonction de l'effort de pêche

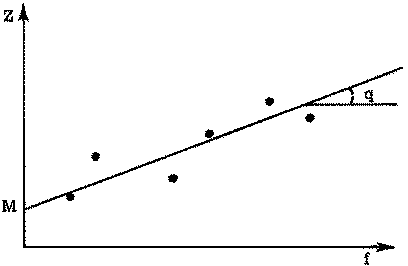
Les techniques normales de régression statistique permettent d'obtenir la solution pour q et M, car l'équation 5.6 se présente sous la forme type de la régression linéaire:

y = a + bx

où y = coefficient de mortalité totale, et x = effort de pêche.

En exprimant par 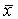et 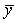les valeurs moyennes de x et de y, on a, par la méthode des moindres carrés, les estimations suivantes de q et de M:

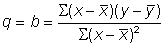, (5.7)

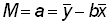, (5.8)

Coefficient de corrélation, niveau de signification de la régression et limites de confiance de M et de q peuvent être calculés par les techniques habituelles.

Les résultats de la régression peuvent être utilisés immédiatement si les coefficients de mortalité ont été estimés à partir d'indices d'abondance à des temps donnés - c'est-à-dire à partir de l'équation 5.1. Ainsi, on peut rapporter la mortalité entre le 1^er janvier 1961 et le 1^er janvier 1962 à l'effort total de pêche en 1961. Le plus souvent, les indices d'abondance dont on dispose ne sont que des moyennes pour une certaine période: par exemple, capture moyenne par unité d'effort en 1961 et 1962. D'après l'équation 5.2, la mortalité estimée à partir du rapport entre les deux indices d'abondance (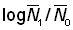) sera liée aux mortalités (et, partant, à l'effort de pêche) dans les deux périodes. Par conséquent, la mortalité doit être rattachée à la moyenne de l'effort de pêche total durant les deux périodes. Ainsi, nous inscrirons sur le graphique le rapport logarithmique des moyennes pour 1961 et 1962 en fonction de l'effort de pêche moyen en 1961 et 1962. On démontre que c'est cette méthode qui permet la meilleure utilisation possible des données (Paloheimo, 1961).

Si la méthode sert évidemment surtout pour la mesure des variations temporelles de l'effort de pêche, par exemple d'une année à l'autre, elle peut également être appliquée lorsque l'effort varie avec l'âge, en supposant que la pêche commerciale emploie un engin sélectif, mais que l'on peut obtenir des indices de densité réelle pour chaque groupe d'âge - par exemple au moyen d'échantillonnages spéciaux effectués par un navire de recherche.

Lorsque les estimations de la mortalité varient beaucoup d'une paire d'années à la suivante, par suite d'erreurs d'échantillonnage ou pour d'autres motifs, (par exemple modifications de la «disponibilité» plutôt qu'en raison de vrais changements dans la mortalité, il est possible d'obtenir un coefficient de mortalité moyen valable pour plusieurs années en suivant l'évolution d'une seule classe d'âge durant sa vie dans sa phase exploitée. Si l'on porte son indice de densité sur une échelle logarithmique, on obtiendra une droite de pente égale au coefficient de mortalité, lequel peut alors être inscrit en fonction de l'effort de pêche moyen durant la période correspondante. Ce procédé réduit la dispersion, mais fait perdre des informations sur l'influence des variations annuelles de l'effort de pêche, sans affecter cependant les tendances à long terme. De plus, les données relatives aux classes d'âge successives provenant pour une large part des mêmes années, les points obtenus ne sont pas tout à fait indépendants, et l'on ne peut pas contrôler exactement, selon les procédés indiqués plus haut, les niveaux de signification et de confiance.

5.4 Mortalité naturelle et allure de la croissance

L'allure de la croissance d'une espèce peut donner une idée de son taux de mortalité naturelle. Un poisson qui parvient rapidement à sa longueur maximale - K élevé - a probablement un haut coefficient de mortalité naturelle M, et inversement. Le rapport entre M et K semble varier d'un groupe de poissons à l'autre: pour les Clupeoidei, M se situe généralement entre 1 K et 2 K; pour les Gadiformes, sa valeur est le plus souvent entre 2 K et 3 K. Ce procédé, comme la méthode de l'aire balayée employée pour l'estimation de la mortalité par pêche, n'est pas précis, mais il se révèle fréquemment précieux aux premiers stades de l'étude d'une pêcherie, pour juger si c'est la mortalité naturelle ou la mortalité par pêche qui l'emporte dans la mortalité totale (Beverton et Holt, 1959).

5.5 Méthodes graphiques spéciales

On peut également avoir recours à des méthodes graphiques pour estimer les taux de mortalité à partir d'autres situations particulières se prêtant mal à l'application de méthodes algébriques. Regier (1962) a décrit des cas de ce genre, où l'on dispose de données de recensement fournissant l'effectif du stock en nombre absolu à diverses époques, ainsi que de statistiques de la prise totale soit durant une très brève campagne (parfois quelques jours seulement, de sorte que la mortalité par pêche est extrêmement élevée), soit durant une période ne représentant qu'une partie du temps écoulé entre les deux dates de recensement.

Examinons d'abord le cas d'une campagne de pêche très courte, durant laquelle on capture 300 poissons, par exemple en deux jours. Supposons qu'à un temps t₀, avant le début de la pêche, le nombre de poissons soit de 1 000, et qu'au temps t₂, après la campagne, il soit tombé à 300. L'emploi de papier semi-logarithmique (figure 5.3) donne l'effectif de la population aux deux dates de recensement: ce sont les points A₀ et A₂. Si les taux de mortalité étaient demeurés constants, la population pendant la campagne de pêche (t₁) aurait été A₁. En fait, les changements réels subis par la population seraient représentés par la ligne A₀ BCA₂ de la figure, où BC représente la capture de 300 poissons, et les deux parallèles A₀B et CA₂ la diminution causée par la mortalité naturelle. Les deux triangles A₀BA₁ et A₁CA₂ étant semblables le rapport des longueurs BA₁: A₁C (mesuré à la règle sur le papier semi-logarithmique) est égal au rapport des époques 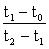Comme première approximation, prenons une position quelconque de C et la position B au point C + 300. Mesurons avec une règle graduée la distance BC (qui variera avec la valeur de C). La distance CA₁, mesurée à la règle, sera alors égale à 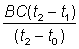. Si l'on obtient une valeur supérieure, c'est que la première approximation de C est trop faible; on peut ainsi rapidement trouver la valeur exacte de C. On détermine alors aisément la mortalité naturelle à partir de la ligne A₀B (ou CA₂): le plus simple est généralement de noter le point où cette ligne intercepte la valeur 1 (ou 100 000) de l'effectif de la population, et de lire cet effectif exactement un an plus tard.

FIGURE 5.3. - Méthode graphique pour déterminer le taux de mortalité.

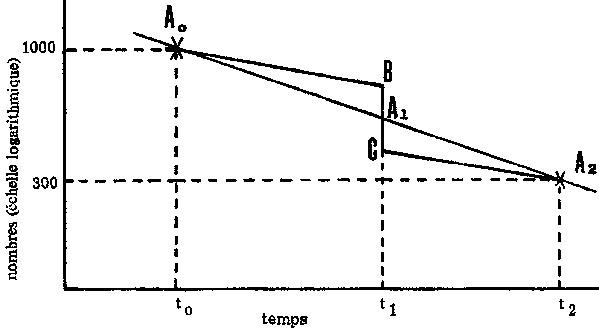
Le plus souvent, la pêche a lieu durant une période - la campagne de pêche - pendant laquelle on peut tenir pour constante la mortalité par pêche. Des dénombrements sont faits à deux dates en dehors de cette campagne, afin que l'intervalle entre les deux recensements comprenne deux périodes, situées l'une avant et l'autre après la pêche, durant lesquelles n'intervient que la mortalité naturelle. En première approximation, on peut supposer que la prise connue C provient toute de la période médiane de la campagne, et la méthode décrite ci-dessus permet d'obtenir une première estimation de la mortalité naturelle: M₁. A partir de cette valeur de M, on calculera les morts survenant en dehors de la campagne de pêche et l'on pourra donc, par soustraction, estimer le nombre total de morts N durant la campagne et la mortalité totale ZT (T étant la durée de la campagne).

On obtiendra alors une estimation de F à partir de l'équation:

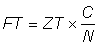
En utilisant cette valeur dans l'équation 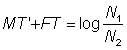, ou N₁ et N₂ sont les nombres aux dates des deux recensements, et T' le temps écoulé entre ceux-ci, on aura une deuxième estimation M₂ de la mortalité naturelle. Une troisième estimation de M est fournie par 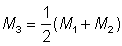, qui peut servir à son tour pour obtenir des estimations améliorées de F et de M. (On appelle itération le procédé qui consiste à obtenir une succession d'estimations de plus en plus approchées).

5.6 Exercices

1. a) Une certaine mortalité provoque chaque année la mort de 25 pour cent de la population. Quel est le pourcentage restant de la population initiale au bout de 2 ans? de 6 mois? de 3 ans? Quel est le coefficient instantané de mortalité correspondant? (N.B.: trouver d'abord le coefficient.) Refaire l'exercice avec des mortalités causant chaque année des pertes de 10, 90, 50 pour cent.

b) Deux causes de mortalité, agissant indépendamment, déterminent des coefficients de mortalité de 0,2 et 0,3. Quel est le coefficient de mortalité totale qui en résulte? Répéter l'exercice avec les coefficients 0,7 et 0,1, puis 1,0 et 0,3.

c) Deux causes de mortalité s'exercent indépendamment sur une population. Par elles-mêmes, elles causeraient respectivement en un an une perte de 20 pour cent et de 30 pour cent de la population. Est-ce que 50 pour cent de la population meurt durant une année? dans la négative, quel est le pourcentage qui meurt effectivement? (N.B.: convertir en coefficients instantanés de mortalité.) Refaire l'exercice avec des mortalités de 70 et de 30 pour cent; de 80 et de 70 pour cent.

d) Tracer y en fonction de x sur du papier semi-logarithmique, et log₁₀ y et Log_e y en fonction de x sur du papier ordinaire, pour chaque ensemble de valeurs de y.

x	0	1	2	3	4	5	6
y1	0,79	0,63	0.50	0,40	0,32	0,25	0,20
y2	0,71	0,35	0,18	0,089	0,045	0,022	0,011

Les points satisfont-ils l'équation ou

log y = ax + b

ou

y == c e^dx ?

Dans l'affirmative, quelles sont les valeurs de a, b, c, d? Les estimer à partir de la pente et du point d'intersection de la droite. Si les y constituent les indices de la densité d'une certaine classe d'âge des poissons à des intervalles annuels, les données correspondent-elles à des coefficients de mortalité constants? Dans l'affirmative, quelles sont les fractions survivantes chaque année, et quels sont les coefficients instantanés de mortalité?

2. En cinq traits de chalut d'une heure, un navire de recherche a capturé les nombres suivants de poissons, respectivement pour chaque catégorie d'âge:

I, 30; II, 450; III, 120; IV, 70; V, 25; VI +, 15;

Un an plus tard, les prises, en 12 traits d'une heure, étaient les suivantes:

I, 60; II, 960; III, 480; IV, 120; V, 72; VI +, 42;

En supposant, aux fins du présent exemple, qu'avec le maillage utilisé la prise par heure donne un indice valable de la densité pour les poissons âgés de 2 ans et plus, estimer le coefficient de mortalité totale pendant l'année. Si l'on dispose de données seulement pour la première des années, estimer la mortalité totale moyenne durant les quelques années précédentes. (Dans la pratique, il ne suffirait généralement pas de 5 à 12 traits pour fournir un indice valable de la densité.)

3. Un groupe de poissons subit pendant deux années consécutives des coefficients de mortalité totale respectifs de 0,85 et 0,80. S'il compte 1 000 individus au début de la première année, quel est le nombre moyen présent durant chacune des deux années? Quel est le coefficient de mortalité totale estimé à partir de ces deux moyennes?

4. Un prélèvement de plancton a montré que 2 × 10¹¹ œufs avaient été pondus durant le frai. Selon des études de fécondité, la femelle mature pond en moyenne 10⁶ œufs. Les études de marché ont fait apparaître pour l'année suivante des mises à terre de 3 millions de poissons, dont 40 pour cent de femelles adultes (ayant pondu au moins une fois). Quel est le pourcentage de femelles frayant capturé pendant l'année? Si le coefficient de mortalité totale est de 1,2 quels étaient le coefficient de mortalité par pêche et le coefficient de mortalité naturelle?

5. Nombre moyen de plies débarquées à Lowestoft par 100 heures de pêche à deux époques différentes:

Années	Age
	2	3	4	5	6	7	8	9	10
1929-38	125	1 355	2352	1 761	786	339	159	70	28
1950-58	98	959	1 919	1 670	951	548	316	180	105

Calculer les coefficients moyens de mortalité totale pendant ces deux périodes. En supposant que les efforts de pêche totaux moyens s'exerçant sur la plie en mer du Nord ont été (en millions d'heures de pêche des chalutiers britanniques à vapeur) 5,0 en 1929-38 et 3,1 en 1950-58, estimer, d'après l'équation 5.6, la mortalité naturelle et la mortalité par pêche durant les deux périodes.

6. Le tableau ci-après donne, pour la mer de Barents, la composition par âge des cabillauds, en nombres débarqués par 100 heures-tonneau par les chalutiers britanniques, et l'effort total de pêche pour chaque année.

Calculer le coefficient de mortalité totale pour chaque paire d'années et pour chaque âge. D'après les données, trouver à partir de quel âge les poissons sont pleinement représentés dans les prises. Quels indices permettent de penser que l'âge au plein recrutement a changé entre l'avant-guerre et l'après-guerre? Trouver une estimation unique de la mortalité entre paires d'années successives (prendre le rapport 7 et plus vieux; 8 et plus vieux). En reliant graphiquement cette mortalité à l'effort de pêche moyen des deux années et en calculant la droite de régression correspondante, estimer la mortalité naturelle et la mortalité par pêche en 1958. Quelles sont les limites de confiance de la mortalité naturelle? (Noter que l'estimation de M obtenue comprendra généralement toute migration nette à partir de la zone exploitée.)

Année	Age
	3	4	5	6	7	8	9	10	11	12+	Effort
1932	0,02	0,38	1,49	3,16	3,81	2,16	1,55	2,20	1,48	2,80	174
1933	-	0,37	2,12	3,37	4,62	3,37	1,60	1,37	0,64	2,18	184
1934	-	0,43	3,18	6,18	5,47	8,69	2,59	0,75	0,56	1,98	164
1935	0,03	0,56	7,85	13,97	10,04	5,82	2,82	0,88	0,29	1,22	184
1936	0,1	0,58	1,75	8,61	7,96	9,28	3,50	0,93	0,19	1,13	252
1937	0,02	1,89	2,91	7,66	17,05	8,65	2,53	0,38	0,26	0,33	321
1938	0,4	1,87	7,09	5,73	9,46	9,54	4,30	1,24	0,48	0,13	253
1946	7,3	11,52	11,39	18,91	13,77	11,77	14,29	17,65	5,26	3,13	66
1947	2,1	18,25	28,42	28,42	22,57	5,99	7,10	10,45	11,01	4,74	103
1948	0,9	1,89	15,59	33,19	26,77	11,31	7,17	2,01	3,65	2,76	156
1949	4,4	12,92	18,38	34,83	20,08	9,08	6,58	2,94	1,59	2,50	171
1950	-	0,49	1,15	5,49	12,89	9,32	4,28	1,76	1,01	0,37	248
1951	0,04	1,41	8,61	13,58	11,52	6,62	4,11	1,76	1,96	0,02	313
1952	0,15	4,65	11,84	16,26	13,14	4,09	2,11	1,52	0,91	0,93	412
1953	0,02	2,02	13,77	16,41	7,20	5,49	1,62	0,70	0,15	0,25	396
1954	0,07	5,33	19,03	21,76	20,25	3,99	1,62	0,48	0,67	0,13	425
1955	-	0,73	10,83	26,82	15,70	5,44	1,93	1,30	0,57	0,19	551
1956	0,02	0,50	6,29	22,76	13,51	5,59	1,20	0,61	0,24	0,08	630
1957	0,08	1,98	3,40	9,81	9,70	6,55	1,29	0,58	0,38	0,10	457
1958	0,6	4,4	9,98	8,31	5,81	5,53	1,56	0,91	0,42	0,20	414