6. MARQUAGE

6.1 Données servant à déterminer les taux de mortalité et la taille de la population
6.2 Variations de la distribution dans l'espace
6.3 Exercices

6.1 Données servant à déterminer les taux de mortalité et la taille de la population

Si le marquage des animaux aquatiques peut servir à l'étude de la croissance, des mouvements ou de migrations, le présent chapitre s'attache uniquement à l'utilisation du marquage en vue de la détermination des taux de mortalité et de la taille de la population (la croissance est traitée au chapitre 3). L'hypothèse la plus simple est que les animaux marqués sont soumis aux mêmes taux constants de mortalité par pêche et de mortalité naturelle que les populations naturelles non marquées; ces taux peuvent donc être estimés séparément puisque, contrairement à celui de la population naturelle, l'effectif initial de la population marquée est connu avec précision.

Autrement dit, si N₀ poissons sont marqués à un certain moment, le nombre N_t en vie après un temps t est donné par la formule:

, (6.1)

Le taux de capture de ces poissons est égal au produit du coefficient de mortalité par pêche par le nombre de poissons vivants, soit:

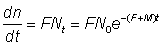
où n = nombre de poissons marqués recapturés.

On obtient le nombre total de recaptures entre le temps t = 0 (date du marquage) et le temps T en intégrant:

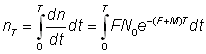
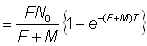
Si les recaptures sont groupées par intervalles de temps de durée T, le nombre n_r pris pendant le r^ème intervalle entre les temps rT et (r + 1) T est:

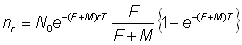, (6.2)

(N.B.: le premier intervalle après le marquage est r = 0).

Le nombre de poissons repris dans les intervalles de temps successifs peut donc être utilisé, connaissant N₀ pour donner des estimations de F et de M. En particulier:

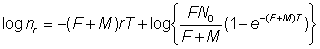, (6.3)

De sorte que, si l'on rapporte log n_r à r, on obtient une droite de pente - (F + M) T. (L'équation 6.9 fournit une autre expression de cette équation, d'un emploi plus commode). En utilisant cette valeur de F + M, on peut estimer F à partir du nombre de recaptures dans un intervalle quelconque, à l'aide de l'équation 6.2, ou à partir de l'intersection avec l'axe des y, celle-ci étant donnée, sur la base de l'équation 6.3, par:

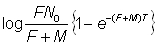
Inversement, le nombre total des recaptures jusqu'au temps t est:

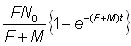
expression à partir de laquelle, en remplaçant F + M, on obtient une estimation directe de F.

Quand t est très grand, cette expression se réduit à .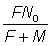

Malheureusement, les suppositions faites dans l'exemple simple qui précède ne se vérifient pas souvent. Les types d'erreurs susceptibles d'apparaître peuvent être classées en catégories bien déterminées selon leurs effets sur les diverses estimations.

1. Erreurs affectant l'estimation du taux de pêche (F), mais non l'estimation de la mortalité totale (type A de Ricker, type 1 de Beverton et Holt):

a) Mort du poisson juste après le marquage;

b) Notification incomplète de récupérations de marques par les pêcheurs (en supposant constante la proportion des récupérations non déclarée; une variation du taux de modification influerait aussi sur l'estimation de la mortalité totale).

2. Erreurs affectant l'estimation de la mortalité totale, mais non celle de la pêche (type B de Ricker, type 2 de Beverton et Holt):

a) Perte des marques (se produisant selon un taux instantané régulier tout au long de l'expérience);
b) Mortalité additionnelle des poissons marqués (intervenant elle aussi tout au long de l'expérience);
c) Migration des poissons marqués.

3. Erreurs affectant à la fois l'estimation de la pêche et celle de la mortalité totale:

a) Vulnérabilité différente à la pêche des poissons marqués et des poissons non marqués - par exemple possibilité accrue que les poissons portant le disque de Peterson soient retenus par un filet;

b) Dispersion non uniforme des poissons marqués au sein de la population non marquée.

Les erreurs de la première catégorie entraînent une sous-estimation de la véritable mortalité par pêche, ce qui en soi peut souvent être utile. Elles sont fréquemment décelables et parfois mesurables par des observations appropriées. Ainsi dans de bonnes conditions, des poissons marqués peuvent être gardés dans des viviers ou des cages, et leur mortalité durant la période suivant le marquage directement observée. Moins directement, on peut comparer les pourcentages de reprise des poissons qui, lors du marquage, étaient dans divers états - plus ou moins vifs, abîmés ou apparemment intacts, etc. - ou avaient été capturés par différentes méthodes. S'il y a mortalité additionnelle due au traumatisme de la capture et du marquage, on peut supposer qu'elle sera plus faible pour des poissons pleins de vie, et plus forte pour des animaux blessés ou endommagés (la perte d'écaillés paraît souvent particulièrement critique). L'absence d'une telle différence pourra être prise, non comme preuve, mais comme indication qu'une telle mortalité additionnelle n'existe guère ou pas du tout.

On peut souvent mettre en évidence la non-déclaration des récupérations de marques en comparant le nombre de marques retournées par unité de quantité de poissons capturés par diverses catégories de navires opérant dans le secteur étudié: bateaux particuliers, différents pays, etc. Pour une mesure directe, on introduira dans les prises des nombres connus de poissons marqués; la technique est couramment utilisée lorsque la récupération se fait mécaniquement (marques aimantées, dans le cas des usines de farine de poisson), mais peut aussi servir, surtout si l'on bénéficie du concours de quelques pêcheurs, pour les marques courantes extérieures récupérées par pêcheurs ou travailleurs de l'industrie à terre.

Les erreurs de la deuxième catégorie peuvent être considérées comme une cause additionnelle de mortalité (autrement dit comme pertes d'individus de la population marquée), de sorte que l'équation 6.1 doit s'écrire:

N_t = N₀ e^-(F+X)t, (6.4)

où X comprend toutes les causes de diminution du nombre des poissons marqués autres que la pêche: perte des marques ou migration aussi bien que mortalité naturelle. L'équation 6.4 et la forme correspondante de l'équation 6.2:

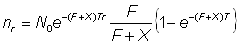, (6.5)

constituent les formules courantes pour l'analyse des résultats de marquage, de sorte qu'en fait seule la mortalité par pêche de la population naturelle sera estimée par le marquage. La mortalité naturelle s'obtiendra par soustraction de la mortalité totale Z, estimée à partir de la composition par âge, etc.

Il est parfois possible d'obtenir une certaine appréciation quantitative des pertes de la catégorie 2: par exemple, les pertes de marques (mais non la mortalité des poissons marqués) peuvent être estimées en fixant deux marques à chaque poisson, puis en notant la proportion de poissons repris avec les deux marques, avec une seule marque, et l'évolution de cette proportion avec le temps.

La vulnérabilité différentielle à la pêche des poissons marqués peut habituellement être éliminée par une conception rationnelle des marques. Il paraît probable que les porteurs de marques du type «bouton» seront particulièrement vulnérables à certains engins, comme les filets fixes: aussi faudrait-il, si possible, éviter l'emploi de ces marques dans les secteurs où l'on pêche avec ce type d'engins. S'il faut les employer, ou encore aux fins d'interprétation d'anciennes données, on pourra estimer l'importance de la mortalité additionnelle par pêche en comparant les taux de reprise des poissons portant divers types de marques.

6.2 Variations de la distribution dans l'espace

L'une des principales difficultés survient lorsque la distribution des poissons marqués diffère de celle de l'ensemble de la population. Si le brassage est relativement rapide, les recaptures d'une période initiale 0 à t', durant laquelle les poissons marqués se mélangent à la population non marquée, pourront être omises dans les calculs. L'étude se fait alors à partir du temps t', avec un nombre initial de marques réduit, en utilisant l'équation 6.1 sous la forme:

N_t = N'₀ e^-(F+X)(t-t') (6.6)

On estime N'₀ à partir du nombre de poissons marqués, en soustrayant le nombre de reprises effectuées pendant la période initiale de mélange et le nombre (estimation) perdu pour toute autre cause, X, cette estimation devant être faite à partir d'une analyse des dernières données. Cependant, il arrive fréquemment que presque toutes les reprises aient lieu avant que les populations marquées et les populations non marquées aient même connu un brassage approximatif.

Ce mélange peut être efficacement accéléré par un mode approprié de marquage. L'objectif est d'obtenir dans toute la population le même rapport poissons marqués/poissons non marqués. On peut l'atteindre par exemple en exécutant un quadrillage régulier de stations de chalutage couvrant la totalité de la surface étudiée, et en marquant tous les poissons capturés à chaque station, ou une proportion constante d'entre eux. Certes, si ce procédé convient à une aire peu étendue, il serait difficile à appliquer par exemple sur l'ensemble de la mer du Nord.

Pour un grand secteur comme la mer du Nord, il peut ne pas être possible d'assurer un bon brassage des poissons marqués et des poissons non marqués. En tous cas, la plupart des récupérations auront déjà eu lieu lorsque celui-ci sera réalisé, et ne pas tenir compte des marques repêchées avant l'achèvement du mélange signifierait rejeter la plupart des données recueillies. Toutefois, si l'on dispose de bons renseignements sur la répartition géographique de l'effort de pêche et sur les emplacements de récupération des marques retournées on peut en tirer d'utiles estimations de la mortalité par pêche subie par la population non marquée. On procédera logiquement comme suit:

a) Estimer la mortalité par pêche F de la population marquée;

b) A partir de la répartition de l'effort de pêche et des poissons marqués, estimer l'intensité de pêche f s'exerçant sur la population marquée;

c) Estimer ensuite q, dans l'égalité F = qf;

d) Estimer l'intensité de pêche s'exerçant sur l'ensemble de la population;

e) Enfin, en supposant que q est le même pour les poissons marqués et pour les poissons non marqués, estimer la mortalité par pêche subie par l'ensemble de la population.

Noter que, particulièrement aux premiers stades, il n'est pas indispensable d'étudier la pêche effectuée par tous les navires, ni dans tous les secteurs, à condition d'utiliser la même partie du total pour calculer la mortalité par pêche (à partir des marques renvoyées) et l'intensité de la pêche (à partir des données sur l'effort). Par exemple, en mer du Nord certaines des données les plus circonstanciées sur l'effort concernent les opérations des chalutiers hauturiers britanniques; il peut donc être pratique de calculer la mortalité par pêche et l'intensité de la pêche uniquement sur la base des renseignements relatifs à ces navires, sans tenir compte des retours de marques et de l'activité halieutique des senneurs et bâtiments de pêche côtière britanniques ou des navires d'autres pays.

Considérons une aire peu étendue autour du point de marquage, dans laquelle le mélange des populations marquées et des populations non marquées se produit rapidement. Pour un certain intervalle de temps i, posons

= nombre moyen de poissons marqués présents
f_i = intensité de pêche (effort par unité de surface par unité de temps)
n_i, = nombre de poissons marqués recapturés

On a:

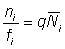, (6.7)

Si l'on rapporte au temps 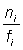(marques récupérées par unité d'intensité de pêche) et si l'on ajuste une courbe aux points obtenus, l'intersection de celle-ci avec l'axe des y sera qN₀ (N₀ = nombre de poissons marqués remis à l'eau). On peut en tirer une estimation de q, et exprimer la mortalité par pêche de l'ensemble de la population par la relation:

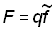
où 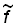est l'intensité de pêche totale effective sur la population, calculée à partir de statistiques détaillées de l'effort de pêche.

Bien que les hypothèses suivantes puissent ne pas être complètement justifiées, on peut, en première approximation, tenir pour constante l'intensité de pêche à l'intérieur de la petite aire choisie autour du point de remise à l'eau, et définir l'émigration hors de cette zone par un coefficient exponentiel constant, D. On aura alors, pour le nombre de poissons marqués dans l'aire au bout d'un temps t, soit N_t:

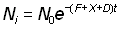
où F est la mortalité par pêche intervenant dans la zone entourant le point de remise à l'eau, et non pas nécessairement celle de l'ensemble de la population. Si le i^ème intervalle dure un temps T, et va du temps 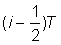au temps :

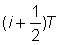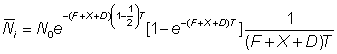
ou encore:

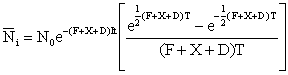, (6.8)

Ainsi, tant que (F + X + D) T est petit, c'est-à-dire tant que les nombres ne changent pas beaucoup durant un intervalle donné, le terme entre parenthèses sera pratiquement égal à l'unité:

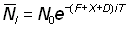, (6.8')

et le tracé de en fonction du temps sur une échelle logarithmique sera une droite. On notera que l'équation 6.8, et plus particulièrement sa forme approchée 6.8', peut être substituée avantageusement à l'équation 6.3 sous la forme:

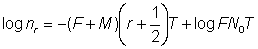
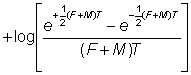, (6.9)

formule où l'on peut, comme précédemment, négliger le dernier terme si les variations des nombres sont faibles dans l'intervalle - autrement dit les logarithmes des nombres de poissons repris durant chaque intervalle portés en fonction du point médian de l'intervalle donneront une droite de pente - (F + M) T coupant l'axe des y au point log FN₀T.

L'équation 6.7 peut être généralisée pour inclure des données provenant d'une aire plus vaste que la petite zone entourant le point de remise à l'eau. En indiquant les valeurs pour des secteurs particuliers par des préfixes adéquats, on a:

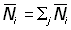
où 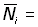nombre total des poissons marqués dans les secteurs étudiés.

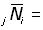nombre des poissons marqués dans le j^ème secteur.

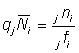
d'où l'on tire:

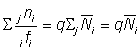, (6.10)

si bien qu'on peut mener l'analyse comme plus haut en utilisant le total des marques retournées par unité d'intensité de pêche dans chaque petit secteur. On ne peut effectuer l'étude que quand on dispose de suffisamment de données sur l'effort de pêche. Si les marques sont renvoyées par plusieurs flottes, dont certaines fournissent des données d'effort valables et d'autres non, seules devront être utilisées dans toutes les analyses les données provenant de la flotte ou des flottes ayant communiqué des renseignements complets du point de vue tant de l'effort que du retour des marques. Les poissons marqués pris par les autres flottes doivent être considérés comme des pertes additionnelles. Les données provenant de ces flottes ne sont prises en considération qu'à la fin, lors du calcul de la mortalité par pêche subie par la population dans son ensemble.

6.3 Exercices

1. Graham (1938) a marqué en mer du Nord 1 000 cabillauds, et l'on a obtenu les récupérations suivantes, groupées par trois mois:

Mois	0-2	3-5	6-8	9-11
Nombres	139	91	52	40

En marquant les logarithmes des nombres d'animaux repris en fonction du temps, estimer les coefficients de mortalité totale et de mortalité par pêche. (Comparer les résultats quand on se sert de l'équation 6.3 et de la forme approchée de l'équation 6.9.)

2. Des merlans marqués et relâchés en mer d'Irlande ont été classés en fonction de leur vivacité et de l'état de leurs écailles. Les nombres de poissons relâchés et de recaptures ont été les suivants (d'après Beverton et Bedford, 1963).

Etat général	Etat des écailles	Nombre de merlans marqués	Nombre de merlans recapturés
Bon	Bon	60	18
Bon	Moyen	98	21
Bon	Mauvais	49	6
Médiocre	Bon	254	60
Médiocre	Moyen	765	159
Médiocre	Mauvais	509	43

Quels sont les indices d'une mortalité due au marquage? En supposant que tous les poissons en bon état ont survécu, quelle est la proportion de morts dans chacune des autres catégories, et quel a été le nombre de poissons effectivement relâchés?

3. Sur des cabillauds marqués et remis à l'eau dans le golfe du Saint-Laurent en 1955, divers pays ont communiqué les nombres suivants de reprises en 1956 (d'après Dickie, 1963):

Pays	Nombre de marques	Débarquements totaux de cabillauds
		tonnes
Canada	392	62400
France	32	28 000
Portugal	29	5 800
Espagne	15	8 100

Calculer le nombre de marques retournées par millier de tonnes de poissons mis à terre dans chaque pays. Quels sont les éléments indiquant que les retours sont incomplets? Si l'on suppose que toutes les marques récupérées par les pêcheurs canadiens sont renvoyées, estimer le nombre réel de reprises des autres pays.

4. Trois groupes de harengs portant des marques intérieures ont été relâchés en mer du Nord pendant l'été de 1957. On dispose de données détaillées sur l'intensité de pêche danoise dans le voisinage des points de remise à l'eau (en heures de pêche par carré statistique - de 15 × 15 milles -). Le tableau suivant indique le nombre de marques retournées et l'intensité de pêche autour de chaque point de marquage durant les semaines consécutives au marquage (d'après des données du CIEM, 1961).

Semaine après le marquage	Nombre de poissons remis à l'eau
	1		2		3
	Nombre de marques	Intensité de pêche	Nombre de marques	Intensité de pêche	Nombre de marques	Intensité de pêche
1	21	80	80	420	3	10
2	35	64	12	60	3	5
3	30	53	10	50	8	15
4	8	26	2	10	2	10
5	10	56	1	10	-	-
Nombre de poissons marqués	3 000		1 500		3 000

Calculer le nombre de marques renvoyées par heure de pêche par carré statistique pour chaque remise à l'eau. D'après cela, si l'on suppose que l'efficacité du système est telle que 90 pour cent des marques récupérées sont renvoyées, quelle est la valeur de q pour une intensité de 100 heures de pêche par carré statistique par semaine?