7.1 Beneficios de la empresa
7.2 Diagramas de flujo de caja
7.3 Métodos de estimación de la rentabilidad
7.4 Consideración del riesgo
7.5 Ventajas y desventajas de los diferentes métodos de estimación de la rentabilidad
7.6 Análisis del punto de equilibrio
7.7 Rentabilidad de las pesquerías artesanales
7.8 Rentabilidad para plantas pesqueras pequeñas y medianas
7.9 Inflación en los cálculos de rentabilidad
La palabra "rentabilidad" es un término general que mide la ganancia que puede obtenerse en una situación particular. Es el denominador común de todas las actividades productivas. Se hace necesario introducir algunos parámetros a fin de definir la rentabilidad. En general, el producto de las entradas de dinero por ventas totales (V) menos los costos totales de producción sin depreciación (C) dan como resultado el beneficio bruto (BB) de la compañía
BB = V - C .......... (7.1)
Cuando se consideran los costos de depreciación, el beneficio neto antes de impuestos (BNAI) resulta:
BNAI = BB - e × IF = V - C - e × IF ......... (7.2)
siendo e = factor de depreciación interno.
Estas ganancias brutas están gravadas impositivamente, de modo tal que el inversor no recibe dicha cantidad de dinero. Estos impuestos constituyen un factor importante para evaluar la economía de cursos alternativos de acción. La presión impositiva es diferente en cada país, por ejemplo (Instituto Francés del Petróleo, 1981):
|
País |
Porcentaje |
|
EE.UU. |
52 |
|
Canadá |
41 |
|
Alemania |
51 |
|
Francia |
50 |
|
Italia |
35 |
|
Reino Unido |
53,75 |
|
Japón |
50 |
Por ejemplo, para el año 1980 en los Estados Unidos, la tasa impositiva es aplicada de la siguiente forma (Jelen y Black, 1983)
|
|
Porcentaje |
|
Tasa sobre los primeros US$ 25 000 de ganancia: |
17 |
|
Tasa sobre los siguientes US$ 25 000 de ganancia: |
20 |
|
Tasa sobre los siguientes US$ 25 000 de ganancia: |
30 |
|
Tasa sobre los siguientes US$ 25 000 de ganancia: |
40 |
|
Tasa para ganancias superiores a US$ 100 000: |
46 |
La misma situación se presenta en países en desarrollo. Por ejemplo, en el año 1969, para Perú, se consideraba la siguiente escala de impuestos (Engstrom et al., 1974):
|
|
Porcentaje |
|
Para ingresos menores de US$ 2 326 |
20 |
|
Ingresos entre US$ 2 326 y 11 628 |
30 |
|
Ingresos mayores a US$ 11 628 |
35 |
Cabe observar que los procedimientos y niveles cambian frecuentemente en algunos países (por ej., anualmente). En términos generales, cuando se desea realizar una estimación aproximada, puede tomarse un porcentaje arbitrario del 40-50% del beneficio neto antes de impuestos. El beneficio neto (BN) de la compañía puede calcularse como:
BN = V - C - e × IF - t × (V - C - d × IF) ......... (7.3)
siendo d = factor de depreciación oficial y t = tasa impositiva.
El movimiento de dinero hacia o desde la empresa se denomina flujo de caja y se define como la diferencia entre ingresos y costos operativos, (sin los costos de depreciación) y después del pago de impuestos; se puede expresar como:
|
FC |
= BN + e × IF = V - C - t × (V - C - d × IF) |
|
|
= BB - t × (V - C - d × IF) |
.......... (7.4) |
El flujo de caja o el beneficio neto no es una medida de la rentabilidad pero estos valores se utilizan para calcular la rentabilidad de un proyecto particular. El objetivo de un inversor o de una compañía es siempre maximizar las ganancias respecto al costo del capital que debe ser invertido para generar dichos ingresos. Si el propósito fuera sólo el de maximizar las ganancias, cualquier inversión que diera beneficios sería aceptable, no importando los bajos retornos o los altos costos.
En estudios económicos donde es necesario comparar entre distintas alternativas de un proyecto y entre la rentabilidad de un proyecto o de las operaciones financieras de plaza, se utilizan métodos de análisis que permiten realizar dicha estimación sobre una base uniforme de comparación.
Todo proyecto de inversión implica una acción a desarrollar durante un determinado número de años en el futuro. El estudio de las características financieras de un proyecto, requiere el análisis de: el valor temporal del dinero, el riesgo financiero, las futuras variaciones del precio de venta, los costos de producción, el volumen de ventas, la tasa impositiva y el tiempo necesario para implementar el proyecto o instalar los equipos antes de comenzar la producción normal y la vida económica del proyecto. Tales factores son los siguientes:
IF = Inversión original fija depreciable
IW = Capital de trabajo
IR = Inversión residual = Terreno + IW
A = Ganancia anual
B = Generación anual de dinero por depreciación
C = Período de construcción
Una forma de visualizar muchos de estos factores, es usar el diagrama de ubicación de caja como el que se muestra en la Figura 7.1 (Perry y Chilton, 1973).
Figura 7.1 Flujo de caja acumulativo de un proyecto
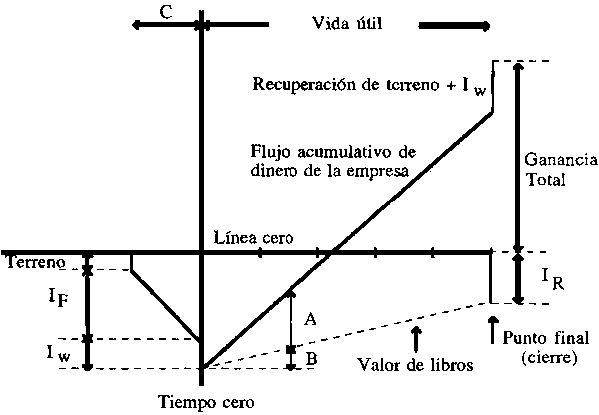
En la Figura 7.1, el dinero es representado en ordenadas y el tiempo en abscisas.
Tiempo igual a cero significa que la planta comienza a producir. A tiempos negativos, el único flujo de caja es negativo, siendo éste el dinero pagado por la tierra y la inversión fija, IF. Cuando el proceso está listo como para comenzar, existe una cantidad de dinero adicional a considerar para el capital de trabajo, IW. Cuando el proceso comienza la producción, el dinero entra al proyecto como producto de las ventas, V. El flujo de caja se acumula entonces, pasando de negativo a positivo y cuando el proyecto termina, el capital invertido en activo de trabajo y terreno es recuperado dando un flujo de caja final positivo.
Este diagrama tiene la ventaja de mostrar todas las características financieras exceptuando: el riesgo, la tasa a la cual es generado el dinero por el proyecto, y las ganancias por re-inversión.
Los esquemas financieros pueden presentarse de modo sencillo haciendo una integración de los datos en los denominados "cuadros de fuentes y usos de fondos". Tales cuadros muestran cuál es el origen o fuente de los fondos y cuál su destino final.
Ejemplo 7.1 Cuadro de fuentes y usos de fondos
Elaborar el cuadro de fuentes y usos para la planta de congelado de merluza del Ejemplo 2.1.
|
Datos: |
IF = US$ 600 000 (del Ejemplo 3.1) |
|
|
IW = US$ 60 000 (del Ejemplo 3.1) |
|
|
Producción diaria = 2 t bloques de filetes congelados (BFC) |
|
|
Días de trabajo al año = 270 |
|
|
n = 10 años |
|
|
Precio de venta = US$ 1 560/t (BFC) |
|
|
Costos unitarios de producción = US$ 1 261/t BFC (Ejemplo 4.4) |
Solución:
|
Ventas anuales |
= Producción anual (t BFC/año) × Precio de venta (US$/t BFC) = |
|
|
= 2 t BFC/día × 270 días/año × 1 560 US$/t BFC = |
|
|
= 540 t BFC/año × 1 560 US$/t BFC = 842 400 US$/año |
|
Costo anual de producción |
= Producción anual (t BFC/año) × Costo unitario de producción (US$/t BFC) |
|
|
= 540 t BFC/año × 1 272 US$/t BFC = 686 880 US$/año |
El método de depreciación utilizado es el método de la línea recta. Los resultados pueden verse en la Tabla 7.1.
7.3.1 Tasa de retorno
7.3.2 Valor presente (VP)
7.3.3 Tasa interna de retorno (TIR)
7.3.4 Tiempo de repago (nR)
Los métodos más comunes de evaluación de rentabilidad son los siguientes:
- Tasa de retorno sobre la inversión original (iROI).
- Tasa de retorno sobre la inversión promedio (iRIP)
- Valor presente (VP)
- Tasa interna de retorno ®.
- Tiempo de repago (nR)
En estudios de ingeniería económica, la tasa de retorno sobre la inversión es expresada normalmente como un porcentaje. El beneficio neto anual dividido por la inversión total inicial representa la fracción que, multiplicada por 100, es conocida como retorno porcentual sobre la inversión. El procedimiento usual es encontrar el retorno sobre la inversión total original siendo
Tabla 7.1 Cuadro de fuentes y usos para una planta pesquera (1990) (en US$ '000)
|
Ejercicio |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
FUENTE |
|
|
|
|
|
|
|
|
|
|
|
Capital propio |
480 |
|
|
|
|
|
|
|
|
|
|
Crédito bancos (*) |
180 |
|
|
|
|
|
|
|
|
|
|
Ventas netas del ejercicio |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
|
Total (a) |
1 502 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
842 |
|
USOS |
|
|
|
|
|
|
|
|
|
|
|
Activo fijo |
600 |
|
|
|
|
|
|
|
|
|
|
Activo de trabajo |
60 |
|
|
|
|
|
|
|
|
|
|
Costos de financiación(**) |
27 |
|
|
|
|
|
|
|
|
|
|
Costos de producción |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
|
Total (b) |
1 374 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
687 |
|
Saldo (a) - (b) |
129 |
156 |
156 |
156 |
156 |
156 |
156 |
156 |
156 |
156 |
|
Beneficio neto (***) |
77 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
93 |
|
Más depreciación |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
60 |
|
Flujo de caja |
137 |
153 |
153 |
153 |
153 |
153 |
153 |
153 |
153 |
153 |
|
Notas: |
(*) Existe un crédito bancario 30 % IF = US$ 180 000 |
|
|
(**) Tasa bancaria, 15% anual. Por simplicidad se ha considerado un crédito de sólo un año. |
|
|
(***) Descontando los impuestos a las ganancias (40%). |
el numerador el valor del beneficio neto promedio:
y de esta manera la tasa de retorno sobre la inversión original, iROI, será:
Sin embargo, debido a la depreciación de los equipos durante su vida útil, a menudo es conveniente referir la tasa de retorno a la inversión promedio estimada durante la vida útil del proyecto. La inversión promedio (IP) se calcula como:
siendo VLk = valor de libros en el año k.
Una fórmula aproximada para calcular la inversión promedio viene dada por:
IP = IF/2 .......... (7.8)
La tasa de retorno sobre la inversión promedio (iRIP) puede ser calculada como:
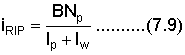
La tasa de retorno sobre la inversión original (iROI) se conoce también como método del ingeniero, mientras que la tasa de retorno sobre la inversión promedio (ic) es un método preferido por los contadores.
Estos métodos dan "valores puntuales" que son aplicables a un año en particular o para algún año "promedio" elegido. No tienen en cuenta la inflación, ni el valor temporal del dinero.
Ejemplo 7. 2 Cálculo de la tasa de retorno sobre la inversión original (iROI)
Calcular la tasa de retorno sobre la inversión para la planta de congelado de merluza del Ejemplo 7.1.
Solución: En este caso donde los flujos anuales de caja no son constantes, se debe calcular:
Beneficio neto anual promedio Flujo anual de caja - Costo anual de depreciación ......... (7.10)
Los valores resultantes se muestran en la Tabla 7.2.
Tabla 7.2 Cálculo del beneficio anual promedio para la planta de la Tabla 7.1
|
Año |
Beneficio neto anual promedio (US$) |
|
1 |
77 000 |
|
2 |
93 000 |
|
3 |
93 000 |
|
4 |
93 000 |
|
5 |
93 000 |
|
6 |
93 000 |
|
7 |
93 000 |
|
8 |
93 000 |
|
9 |
93 000 |
|
10 |
93 000 |
|
Total |
914 000 ÷ 10 = 91 400 |
La tasa de retorno promedio sobre la inversión original será:
(91 400/660 000) × 100 = 13,8 % por año
El valor temporal del dinero no es considerado, ya que se utiliza el beneficio promedio, no su secuencia en el tiempo. Alterando el orden de las ganancias para los años 1 a 10, el retorno sobre la inversión original sería el mismo.
Ejemplo 7.3 Cálculo de la tasa de retorno sobre la inversión promedio (iRIP)
Calcular la inversión residual promedio para la planta de congelado de merluza del Ejemplo 7.1.
Solución: Para determinar correctamente la inversión promedio se debe calcular la inversión residual promedio de acuerdo a la Tabla 7.3.
De la Tabla 7.3, el divisor de la Ecuación (7.9) es:
IP + IW = US$ 330 000 + US$ 60 000 = US$ 390 000
y la tasa de retorno sobre la inversión promedio, será:
Tabla 7.3 Cálculo de la inversión promedio para la planta de la Tabla 7.1
|
Ano |
Inversión (US$) |
|
1 |
600 000 |
|
2 |
600 000 - 60 000 = 540 000 |
|
3 |
540 000 - 60 000 = 480 000 |
|
4 |
480 000 - 60 000 = 420 000 |
|
5 |
420 000 - 60 000 = 360 000 |
|
6 |
360 000 - 60 000 = 300 000 |
|
7 |
300 000 - 60 000 = 240 000 |
|
8 |
240 000 - 60 000 = 180 000 |
|
9 |
180 000 - 60 000 = 120 000 |
|
10 |
120 000 - 60 000 = 60 000 |
|
Total |
3 300 000 ÷ 10 = 330 000 |
Puede observarse que, de hacer una aproximación con la fórmula (7.8):
lo que representa un 8,5 % de error en la estimación. El valor temporal del dinero no es considerado, ya que se usó la inversión promedio, no su secuencia en el tiempo.
Este método compara los valores presentes (VP) de todos los flujos de caja con la inversión original. Supone igualdad de oportunidades para la re-inversión de los flujos de caja a una tasa de interés pre-asignada. Esta tasa puede tomarse como el valor promedio de la tasa de retorno que obtiene la compañía con su capital o se lo puede designar como el retorno mínimo aceptable para el proyecto. El valor presente del proyecto es igual a la diferencia entre el valor presente de los flujos anuales de fondos y la inversión inicial. El valor presente neto es una única cantidad referida al tiempo cero y representa un premio si es positiva, o un fracaso si es negativa, para una tasa de interés elegida.
Otra forma de definir el valor presente, es la cantidad adicional que será requerida al comienzo del proyecto, usando una tasa de interés pre-asignada, para producir ingresos iguales a, y al mismo tiempo que, la inversión total. Los resultados no indican la magnitud del proyecto. Por esa razón, se define una variante del valor presente como la relación entre el valor presente de los flujos anuales de fondos y la inversión total (Ecuación 7.12)
Esta relación puede utilizarse como un indicador de la rentabilidad del proyecto, analizando el alejamiento del resultado con respecto al valor unitario. La unidad corresponderá al caso en que la tasa pre-asignada coincida con el valor de la tasa interna de retorno (ver punto 7.3.3.). Los resultados de ambos cálculos (Ecuaciones 7.11 y 7.12) pueden dar una idea de la magnitud total del proyecto.
Ejemplo 7.4 Cálculo del valor presente (VP)
Calcular: (a) el valor presente (VP) y (b) la relación VP' para la planta de congelado de merluza del Ejemplo 7.1.
Solución: En este caso, considerando una tasa i = 15% anual en la Ecuación (7.11), se obtienen los siguientes resultados:
Se debe notar que el valor residual y el capital de trabajo se deben incluir en el flujo de caja del último año.
(a) VP = US$ 772 182 - US$ 660 000 = US$ 110 182
Al final de los 10 años, el flujo de caja del proyecto, compuesto sobre la base de ingresos al final del año, serán:
F = 137 000 (1,15)9 + 153 000 (1,15)8 + 153 000 (1,15)7 + 153 000 (1,15)6 + 153 000(1,15)5 + 153 000 (1,15)4 + 153 000 (1,15)3 + 153 000 (1,15)2 + 153 000 (1,15) + 213 000 = US$ 3 115 816
Esta suma representa el valor futuro de los flujos del proyecto y debe ser igual al valor futuro de la inversión inicial más el valor presente compuesto a un interés anual del 15%.
F = (660 000+110 182) × (1,15)10 = US$ 3 115 816
En este ejemplo, US$ 110 182 es la cantidad que sumada a la inversión (US$ 660 000) dará la suma que debería invertirse al 15% para obtener ingresos anuales iguales a, y al mismo tiempo que los estimados por la inversión recomendada.
(b) La relación entre el valor presente de los flujos anuales de fondos y la inversión total, de la Ecuación (7.12):
Este método tiene en cuenta la valorización del dinero invertido con el tiempo y está basado en la parte de la inversión que no ha sido recuperada al final de cada año durante la vida útil del proyecto.
Se utiliza un procedimiento de prueba y error para establecer la tasa de interés que debería aplicarse anualmente al flujo de caja de tal manera que la inversión original sea reducida a cero (o al valor de venta más terreno más capital de trabajo) durante la vida útil del proyecto.
Por lo tanto, la tasa de retorno que se obtiene es equivalente a la máxima tasa de interés que podría pagarse para obtener el dinero necesario para financiar la inversión y tenerla totalmente paga al final de la vida útil del proyecto.
En consecuencia, en este método se especifica el valor presente de todos los flujos de caja igual a cero y la tasa interna de retorno, r, se calcula por prueba y error:
Tasa interna de retorno = TIR = r, donde:
Debe destacarse que la preparación de estudios de factibilidad se realiza usualmente por computadora. Los programas de computadora para estimar la rentabilidad tienen una amplia variedad de usos, aumentando la precisión y reduciendo el tiempo y el costo de la preparación de las estimaciones de la inversión y los beneficios.
Ejemplo 7.5 Cálculo de la tasa interna de retorno ®
Calcular la tasa interna de retorno para la planta de congelado de merluza del Ejemplo 7.1.
Solución: Al final de los 10 años, el valor presente de los flujos de caja (expresados dólares) será,
que deberá igualar al valor presente de la inversión inicial fija más el capital de trabajo.
VP = IF + IW = US$ 660 000 .......... (7.15)
Haciendo la (7.14) igual a la (7.15) y buscando por prueba y error el valor de r, se obtiene la tasa interna de retorno. Esta búsqueda por prueba y error puede resolverse por computadora pero en su defecto, el procedimiento normalmente utilizado consiste en aplicar un factor de descuento a los flujos de cajas anuales y sumar de tal forma de obtener el valor presente probando con distintos valores de r hasta obtener el valor de la inversión requerida.
El factor de descuento para pagos al final del año M, es:
|
donde: |
r = tasa de interés elegida |
|
|
M = año para el que se realiza el cálculo. |
En la Tabla 7.4 se muestra el método de prueba y error utilizado en el caso del ejemplo.
La interpolación para determinar el valor de r correcto puede realizarse graficando la relación entre la inversión original y el valor presente total en función de r, como se muestra en la Figura 7.2.
En la Tabla 7.4 se han omitido algunas columnas del factor dM por simplicidad. Esta tasa de retorno de 19,1% es la tasa de interés a la que el dinero original de US$ 660 000 podría ser invertida para proporcionar ingresos tales y al mismo tiempo que los calculados para la inversión propuesta. Así,
1) 660 000 × 1,191 = 785 697; 785 697 - 137 000 = 648 697
2) 648 697 × 1,191 = 772 241; 772 241 - 153 000 = 619 241
3) 619 241 × 1,191 = 737 136; 737 136 - 153 000 = 584 176
4) 584 176 × 1,191 = 695 432; 695 432 - 153 000 = 542 432
5) 542 432 × 1,191 = 645 738; 645 738 - 153 000 = 492 738
6) 492 738 × 1,191 = 586 580; 586 580 - 153 000 = 433 580
7) 433 580 × 1,191 = 516 156; 516 156 - 153 000 = 363 156
8) 363 156 × 1,191 = 432 319; 432 319 - 153 000 = 279 319
9) 279 319 × 1,191 = 332 515; 332 515 - 153 000 = 179 515
10) 179 515 × 1,191 = 213 000; 213 000 - 213 000 = 0
Tabla 7.4 Cálculo de la tasa interna de retorno para la planta pesquera del Ejemplo 7.1
|
Año (m) |
Flujo de Caja |
Prueba para r = 0,1 |
Prueba para r = 0,2 |
r = 0,19 |
|||
|
Factor dm |
Valor presente (US$) '000) |
Factor dm |
Valor presente (US$) '000) |
Factor dm |
Valor presente (US$) '000) |
||
|
0 |
(660) |
|
|
|
|
|
|
|
1 |
137 |
0,909 |
125 |
0,833 |
114 |
0,840 |
115 |
|
2 |
153 |
0,826 |
126 |
0,694 |
106 |
0,705 |
108 |
|
3 |
153 |
0,751 |
115 |
0,579 |
89 |
0,592 |
91 |
|
4 |
153 |
0,683 |
104 |
0,482 |
74 |
0,497 |
76 |
|
5 |
153 |
0,621 |
95 |
0,402 |
61 |
0,417 |
64 |
|
6 |
153 |
0,564 |
86 |
0,335 |
51 |
0,350 |
54 |
|
7 |
153 |
0,513 |
78 |
0,279 |
43 |
0,294 |
45 |
|
8 |
153 |
0,466 |
71 |
0,232 |
35 |
0,247 |
38 |
|
9 |
153 |
0,424 |
65 |
0,194 |
30 |
0,207 |
32 |
|
10 |
213 |
0,385 |
82 |
0,162 |
35 |
0,174 |
37 |
|
Total |
|
|
948 |
|
638 |
|
600 |
|
|
1,44 |
|
0,97 |
|
1,00 |
||
Figura 7.2 Interpolación para el cálculo de la r, con los valores de la Tabla 7.4
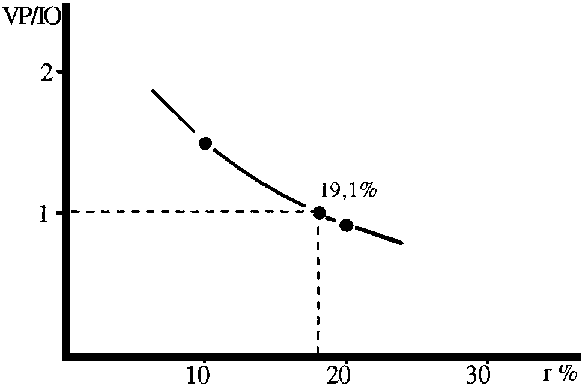
Es necesario destacar que la tasa interna de retorno calculada para la planta del ejemplo es menor que las tasas observadas en plantas similares de mayor escala. Este resultado, concordante con la realidad, tiene su justificación en los conceptos descriptos en el Capítulo 5.
Se define como el mínimo período de tiempo teóricamente necesario para recuperar la inversión original en forma de los flujos de caja del proyecto. Generalmente, la inversión original significa sólo la inversión fija inicial depreciable.
Ejemplo 7.6 Cálculo del tiempo de repago (nR)
Calcular el tiempo de repago para la planta de congelado de merluza del Ejemplo 7.1.
Solución: La aplicación de este método a los datos de la Tabla 7.1, da el tiempo requerido para reducir la inversión a cero. De la ecuación (7.17):
el cual es un valor aproximado, que sólo coincide con el valor real cuando los flujos de caja son iguales. En la Tabla 7.5 se muestra que la inversión se reducirá a cero entre los años 4 y 5.
Tabla 7.5 Flujo de caja acumulado para la planta de la Tabla 7.1
|
Año |
Flujo de caja (US$) |
Rujo de caja acumulado (US$) |
|
0 |
- 600 000 |
- 600 000 |
|
1 |
137 000 |
- 463 000 |
|
2 |
153 000 |
- 310 000 |
|
3 |
153 000 |
- 157 000 |
|
4 |
153 000 |
- 4 000 |
|
5 |
153 000 |
149 000 |
|
6 |
153 000 |
302 000 |
|
7 |
153 000 |
455 000 |
|
8 |
153 000 |
608 000 |
|
9 |
153 000 |
761 000 |
|
10 |
153 000 |
914 000 |
Los valores de la Tabla 7.5 se graficaron en la Figura 7.3. Esta figura permite la interpolación gráfica obteniéndose un valor de tiempo de repago igual a 4,05 años que es el valor real de nR.
Figura 7.3 Interpolación gráfica para la obtención del tiempo de repago
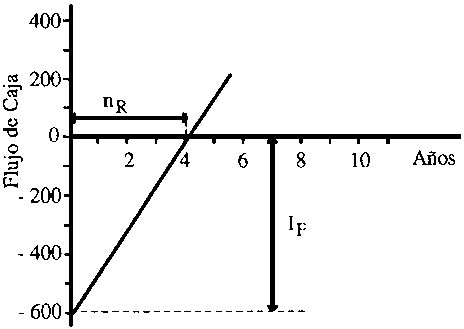
Las inversiones de capital se realizan con la expectativa de obtener una sustancial rentabilidad anual, pero siempre existe la posibilidad que se produzcan pérdidas. Este hecho es lo que se denomina el "riesgo" que acompaña a toda inversión. En general, cuanto mayor es el riesgo, mayor es la tasa de retorno esperada y menor el tiempo previsto para la recuperación de la inversión.
La Tabla 7.6, que consigna valores promedios de tasas anuales de retorno libres de riesgo en las inversiones de capital de industrias de proceso, nos permite la comparación con los resultados de nuevos estudios de factibilidad en la ampliación o modificación de plantas existentes (Rudd y Watson, 1976; Woods, 1975).
A partir de la ecuación (7.3), con d igual a e y constantes, se define el beneficio neto riesgoso (BNR) como:
BNR = (V - C - d × IF) × (1 - t) - iM × (IF + IW) .......... (7.20)
Tabla 7. 6 Valores promedio de la rentabilidad del capital libre de riesgo para industrias de proceso
|
Industria |
Tasa anual, (%) |
|
Servicios públicos (electricidad y gas) |
6,3 |
|
Empresas telefónicas |
6,8 |
|
Aceros (EE.UU) |
7,5 |
|
General Motors |
7,8 |
|
Standard Oil |
8,2 |
|
Celulosa y papel, caucho |
8 - 10 |
|
Fibras sintéticas, productos químicos y petróleos |
11 - 13 |
|
Drogas y productos farmacéuticos, industria extractiva y minería |
16 - 18 |
En la Tabla 7.7, se muestra la tasa de rentabilidad mínima aceptable (iM) en función del grado de riesgo del tipo de proyecto (Happel y Jordan, 1981).
Tabla 7.7 Cuantificación del riesgo
|
Tipo de proyecto |
Grado de riesgo |
iM (%) |
|
Proyectos cortos, modificación de plantas existentes, capital de trabajo, terreno |
Bajo |
10-15 |
|
Equipos específicos |
Moderado |
15-25 |
|
Nuevas instalaciones para un nuevo producto |
Alto |
20-50 o más |
Un resultado mayor que cero indica que el proyecto posee una rentabilidad anual que supera la tasa mínima aceptable, aún considerando el riesgo. Este método no tiene en cuenta el valor temporal del dinero, pero existen expresiones más completas en la bibliografía, como el método del valor del riesgo (Happel y Jordan, 1981).
Ejemplo 7.7 Cálculo del beneficio neto riesgoso (BNR)
Calcular el beneficio neto riesgoso para la planta de congelado de merluza del Ejemplo 7.1.
Solución: De la Tabla 7.7 se seleccionó una tasa de rentabilidad mínima aceptable del 10% por considerarse una alternativa de bajo riesgo. De la Ecuación (7.20):
BNR = 91 400 - 0,10 × 660 000 = US$ 25 400
El resultado mayor que cero indica que el proyecto posee una rentabilidad anual que supera la tasa mínima aceptable, aún considerando el riesgo. Queda al lector la determinación de la rentabilidad para la planta de conservas del Ejemplo 2.2 en forma similar a los Ejemplos 7.1 a 7.7.
|
Datos: |
IF = US$ 130 000 (del Ejemplo 3.2) |
|
IW = US$ 13 000 (del Ejemplo 3.2) | |
|
Producción diaria = 2 670 latas | |
|
Días de trabajo al año = 250 | |
|
n = 10 años | |
|
Precio de venta = US$ 0,8/lata | |
|
Costo unitario de producción = US$ 0,68/lata (Ejemplo 4.5) | |
|
Depreciación por el método de la línea recta. |
Los métodos de retorno sobre la inversión fija o sobre la inversión promedio dan valores estáticos que pueden arrojar resultados ilusorios. Estos "valores puntuales" son tanto aplicables para un año en particular como para un año "promedio". No obstante, son los más sencillos para una estimación rápida. El tiempo de repago no considera apropiadamente los últimos años de la vida útil del proyecto. Por otra parte, el método de la tasa interna de retorno tiene en cuenta la modificación del valor del dinero con el tiempo y brinda resultados más reales que los otros métodos. Si se tienen inversiones posteriores, el valor presente es el método a utilizar, ya que el método de la tasa interna de retorno da soluciones múltiples.
Ante la pregunta: ¿Cuál es el mejor criterio de rentabilidad?, la respuesta es, que en la práctica el analista no usará un solo criterio, sino que considerará el empleo de varios criterios para compensar las ventajas y desventajas de cada uno. La Tabla 7.8 indica los valores razonables del tiempo de repago y de la tasa interna de repago para proyectos con distintos grados de riesgo (Cunningham, 1980).
Tabla 7.8 Valores típicos del tiempo de repago y de la tasa interna de retorno en función del riesgo
|
Proyecto |
Tiempo de repago (años) |
Tasa interna de retorno (%) |
|
Riesgoso |
< 2 |
> 20 |
|
Normal |
< 5 |
15 |
|
Poco riesgo |
|
< 10 |
En general, para plantas pesqueras, los factores claves que afectan la rentabilidad de la operación en plantas pesqueras son: el costo y calidad de la materia prima y el rendimiento del procesamiento, siempre que exista disponibilidad de materia prima y estabilidad en el mercado para los productos resultantes (Montaner y Zugarramurdi, 1994).
El análisis del Punto de Equilibrio es un método para organizar y presentar algunas de las relaciones estáticas de una empresa en el corto plazo. Las cartas económicas de producción muestran cómo los costos, ventas y ganancias variarán cuando cambia el nivel de producción, mientras otros factores permanecen constantes. Estas evaluaciones no tienen en cuenta el valor temporal del dinero y se acepta que los datos utilizados para las decisiones son confiables.
El modelo más conocido de punto de equilibrio relaciona los costos fijos y variables con los ingresos por ventas con el fin de planificar los beneficios. En la mayoría de los casos, la eficiencia de las operaciones de producción depende de la utilización de la planta. Cuando el beneficio puede ser definido como una función del nivel de producción del sistema, es posible seleccionar el nivel de producción para el cual el beneficio será máximo. Matemáticamente, los cálculos son:
- Ventas totales = Precio de venta (US$/unidad) × Nivel de producción (unidades/tiempo) = P × Q.......... (7.21)- Costos totales = Costo variable (US$/unidad) × Nivel de producción (unidades/tiempo) + Costo fijo total (US$/tiempo) = V × Q + CFT.......... (7.22)
- Beneficio neto antes de impuestos = BNAI = Ventas totales - Costos totales = P × Q - (V × Q+ CFT).......... (7.23)
En el punto de equilibrio, los beneficios se igualan a cero y la producción para el punto de equilibrio se puede calcular como:
Q = CFT/(P - V) .......... (7.24)
El valor de Q indica el volumen al cual las ventas y los costos de producción se igualan exactamente. En este punto, una unidad adicional producida y vendida produciría una ganancia. Hasta que el punto de equilibrio es alcanzado, el productor opera a pérdida. Debe resaltarse el efecto del nivel de producción y del tiempo de operación sobre los costos. Considerando la demanda de ventas junto con la capacidad y las características de operación de los equipos, el evaluador puede recomendar el nivel de producción y los esquemas de producción que brinden los mejores resultados económicos.
Usualmente es aceptado que las empresas buscan obtener la mayor utilidad posible. La mayoría de las teorías microeconómicas se basan en el criterio de considerar a la empresa como un ente maximizador de ganancias. En el corto plazo, durante el cual el nivel de producción puede variar pero no el tamaño de la planta, la empresa se enfrenta con diferentes alternativas de niveles de producción, cada una con diferentes beneficios, tal que puede seleccionar la alternativa con los mayores ingresos esperables.
El tratamiento teórico depende de las características del mercado. En un mercado de competencia perfecta se sabe que el precio de equilibrio de mercado de un producto es alcanzado a un nivel de producción del sector industrial QT y a un precio P*. Esto significa que cada empresa tiene una curva de demanda horizontal, que intercepta al eje vertical al precio de equilibrio (P*) establecido por las curvas de oferta y de demanda del mercado. En este caso, tanto los ingresos marginales como los ingresos promedio son constantes y P* = VM = VP.
Estas relaciones se muestran en la Figura 7.4.
Figura 7.4 Equilibrio a corto plazo para una empresa en un mercado de competencia perfecta
Dado que la empresa puede vender cualquier cantidad de producto (Q) al mismo precio, su función de ventas totales (VT), será una recta con pendiente positiva, que comienza en el origen. Si la empresa tiene una estructura de costos representadas por las siguientes curvas de costos: totales promedios (CTP), marginales (CM) y totales (CT); ¿Qué cantidad total decidirá la firma ofrecer para la venta y cuál será su beneficio en ese caso?
La respuesta a estas preguntas requiere la consideración de las metas de una empresa produciendo en un entorno de competencia perfecta: maximizar el beneficio o minimizar las pérdidas. La forma más sencilla de determinar el punto en el cual los beneficios son maximizados es comparar las ventas totales y los costos totales o igualar los ingresos marginales (VM) y los costos marginales (CM). Este razonamiento está mostrado en la Figura 7.4. La empresa maximiza su ganancia vendiendo una cantidad (Q*) para la cual CM = P*. La distancia vertical entre la recta de ventas totales y la curva de costos totales indica la ganancia. Esta será máxima cuando Q* es el número de unidades producidas. La función beneficio de la empresa se deriva restando CT de las VT para cualquier nivel de producción. En este esquema también es posible incurrir en pérdidas en el corto plazo, dependiendo del nivel de precios del mercado, y aún así continuar produciendo, dado que esta alternativa ofrece menores pérdidas que el cierre de la planta.
La Figura 7.5 muestra el caso de una empresa que se enfrenta con menores y menores P. Que la firma se encuentre con pérdidas o ganancias depende de la relación entre el precio y el costo total promedio en la intersección de las VM y los CM. Las cantidades a producir (Qd, Qc, Qb y Qa) para cada diferente nivel de precios (Pd, Pc, Pb y Pa) están determinadas por:
Precio = Costo marginal
- El punto (Qd, Pd) maximiza el beneficio debido a que el precio Pd excede a CTP.- El punto (Qc, Pc) es un punto de equilibrio, ya que el beneficio es igual a cero. El precio Pc iguala a los CTP.
- El punto (Qb, Pb) minimiza las pérdidas en el corto plazo debido a que el precio Pb es menor que CTP.
- El punto (Qa, Pa) es el punto de cierre, los beneficios negativos igualan los CFT o Pa = CVP. Se incurrirá en pérdidas en el corto plazo iguales a los costos fijos totales si la producción se cierra temporariamente.
Figura 7.5 Curva de oferta en el corto plazo para una empresa en un mercado de competencia perfecta
Esta conclusión es útil para derivar la curva de oferta de la empresa en el corto plazo, como se observa en la Figura 7.5. La curva de oferta que maximiza la ganancia de la empresa es la curva ascendente de costo marginal.
En el corto plazo, una empresa encuentra su capacidad limitada por los insumos fijos, mientras que en el largo plazo las opciones son numerosas: puede alterar su tamaño, implementar nuevas tecnologías, o modificar las características de sus productos, de acuerdo con los cambios de los gustos del consumidor. Como extrapolación de estos conceptos, cada empresa puede determinar su curva de oferta a largo plazo. En condiciones reales, existen variaciones dependiendo de la estructura de la competencia, es decir, si existen pocos o muchos oferentes, o dependiendo si los productos son idénticos o diferenciados. Visto desde esta perspectiva pueden encontrarse cuatro tipos de estructura de mercado:
- Competencia perfecta: muchos vendedores de un producto estandarizado.
- Competencia monopólica: Muchos vendedores de un producto diferenciado.
- Oligopolio: Pocos vendedores de un producto estándar o diferenciado.
- Monopolio: Unico vendedor de un producto que no tiene sustituto.
Ejemplo 7.8 Determinación del punto de equilibrio para una planta de congelado de pescado
Analizar la planta de congelado de merluza del Ejemplo 2.1. Graficar las curvas de costos totales, ingresos por ventas y beneficio total. Determinar el punto de equilibrio de dicha planta.
Solución: Datos:
Precio de venta = US$ 1 560/t bloques de filetes congelados
Costo unitario de producción = US$ 1 272/t BFC (Ejemplo 4.4)
Costo variable unitario = US$ 1 085,5/t BFC (Ejemplo 4.4)
Costo fijo unitario = US$ 186,5/t BFC
Capacidad diaria = 2 t BFC
Días de trabajo anuales = 270
Las ecuaciones (7.21) y (7.22) se aplican para calcular VT, CVT, CFT, CT y BNAI sobre un rango de 0 a 100% de producción.
- Ventas anuales = US$ 1 560/t BFC × Q (t BFC/año) = 1 560 × US$ Q/año- Costo anual de producción = US$ 1 085,5/t BFC × Q (t BFC/año) + US$ 186,5/t BFC × 540 t BFC/año = US$ (1085,5 × Q + 100 710)/año
De la Ecuación (7.24), el punto de equilibrio puede calcularse como:
N = 100 710/(1 560 - 1 085,5) = 210 t BFC/año
En la Tabla 7.9 y en la Figura 7.6, se muestran las curvas de costos totales, ingresos por venta y el punto de equilibrio.
Tabla 7.9 Ingresos, costos y beneficios anuales para distintos niveles de producción
|
Porcentaje de Utilización |
Q (t/año) |
VT (US$ '000) |
CVT (US$ '000) |
CFT (US$ '000) |
CT (US$ '000) |
BNAI (US$ '000) |
|
0 |
0 |
0 |
0 |
100,71 |
100,71 |
- 100,71 |
|
20 |
108 |
168,48 |
117,23 |
100,71 |
217,94 |
- 49,46 |
|
40 |
216 |
336,96 |
234,47 |
100,71 |
335,18 |
1,78 |
|
60 |
324 |
505,44 |
351,70 |
100,71 |
452,41 |
53,03 |
|
80 |
432 |
673,92 |
468,94 |
100,71 |
569,65 |
104,27 |
|
100 |
540 |
842,40 |
586,17 |
100,71 |
686,88 |
155,52 |
La Figura 7.6 ilustra la relación anual entre los costos fijos y los costos totales y el nivel de producción, así como la relación entre las ventas y el nivel de producción.
Para una carta lineal de punto de equilibrio, la operación rentable se encuentra a la derecha del punto de equilibrio (39% de utilización de la planta o 210 t BFC por año o 0,78 t BFC por día). Si la producción está por debajo, la operación da pérdidas y por encima, se obtienen ganancias.
Figura 7.6 Representación gráfica del punto de equilibrio para una planta de congelado de merluza
Ejemplo 7.9 Determinación del punto de equilibrio para una planta de harina de pescado
Analizar el punto de equilibrio para la planta de harina del Ejemplo 5.3., que procesa diariamente 500 t de materia prima.
Solución: En la Figura 7.7 se muestra el gráfico de punto de equilibrio para los valores de la Tabla 5.6, en el caso de la planta de 500 t/día.
Figura 7.7 Gráfico de punto de equilibrio para una planta de harina de 500 t/día
En las pesquerías artesanales que explotan un elevado número de especies, con frecuencia los precios son fijados por o para distintas especies, pero de un mismo tamaño. Estos grupos pueden o no tener características biológicas similares. En las variedades comerciales el precio es asignado en forma directamente proporcional a las preferencias del consumidor. Generalmente, estos precios son estables, aunque pueden cambiar substancialmente durante ciertas estaciones, por variación en el volumen capturado, por mezcla de especies, o con anterioridad a eventos tradicionales o religiosos. Por consiguiente, hay una diferencia en los ingresos recibidos por todos y cada uno de los tipos de empresas en el curso de un año dado (Stevenson et al., 1982).
Para mejorar el balance económico, los países apoyan a las pequeñas pesquerías con distintos modos de financiación. Por ejemplo, en Ghana y Senegal, el Gobierno ha puesto en práctica un sistema enfocado substancialmente a la reducción de los impuestos sobre los combustibles utilizados por las embarcaciones y canoas durante más de 10 años. Esta política de disminución de los costos de operación, influye favorablemente para la motorización en ambos países. En Ghana, la reducción es de US$ 0,80/litro a US$ 0,25/litro, mientras que, en Senegal, es menos de la mitad del precio regular de US$ 0,50/litro.
Debe tenerse en cuenta que algunas veces esta política puede causar distorsiones, pues se compran motores más grandes de los necesarios y se usan guinches activos en vez de estáticos, con lo cual se incrementan los costos de operación del sector y de la economía como un todo (Greboval, 1989).
Otro estudio realizado en Seychelles (Parker, 1989) mostró que si existen dificultades económicas en las embarcaciones pequeñas, también las sufren aquellas embarcaciones entre 8 a 13 metros de eslora, a causa de la mayor cantidad de capital invertido en cada unidad pesquera. Por ello, se analiza el rendimiento económico de tres unidades de este tipo de embarcaciones:
1. Modelo estándar (con motor de 27 hp a 37 hp)2. Modelo estándar con eco-sonda y reels eléctricos (seleccionado porque obtuvo la mejor captura), motor de 56 hp.
3. Similar al segundo modelo, de igual capacidad pero con motor de 70 hp (11,6 m de eslora).
Los ingresos de un viaje individual pueden ser considerados en función de los precios, velocidades de captura alcanzada por las artes de pesca utilizadas, composición de la captura y duración del viaje (sujeto a las limitaciones de la capacidad de mantenimiento del barco). En el primer caso, el ingreso estimado por viaje es US$ 1 558 y para los otros, de US$ 2 833.
El parámetro más importante en relación con los ingresos totales es el número de viajes que el barco puede realizar en un período de tiempo dado. Los gastos operativos y financieros se afrontan con más facilidad si el barco es operado más intensivamente. Sin embargo, la falta de un mantenimiento adecuado, reducirán los flujos de caja. Un flujo de caja pequeño reduce la disponibilidad de fondos para mantenimiento y se crea un círculo vicioso.
La pregunta de cuál es la tasa de retorno razonable para el propietario del bote es discutible, dado que la tasa de interés bancaria para aquel pescador que solicita un crédito es del 10% o superior (aunque podrían ser respetables para aquéllos quienes están acostumbrados a manejar grandes capitales).
Es dificultoso administrar una inversión que da sólo el 14% cuando se tiene que pagar el 10% por préstamos. Por ello, se analizó en la Tabla 7.10 la forma de revertir la situación, eliminando un impuesto a los combustibles (columna 3), incrementando los precios pagados por la captura en un 10% (Columna 4) y los dos efectos juntos (Columna 5). Para la embarcación estándar, se ha considerado el caso de 2 y 2,5 viajes por mes, mientras que para las embarcaciones 2 y 3 solamente la mayor cantidad de viajes. Para los propietarios de las embarcaciones es prácticamente imposible enfrentar el pago de los préstamos para cambiar por motores de mayor capacidad (Embarcación 3), sin aumento en los precios de venta de las capturas o disminución de los costos operativos (Parker, 1989).
En las costas de Karnataka (India), (Nordheim et al., 1980), como parte de un programa de la FAO para incrementar y mejorar la utilización de pequeños pelágicos, se estudió el uso de agua de mar refrigerada (AMR) en el manipuleo y traslado de especies pelágicas (caballa y sardina), con la finalidad de aumentar su utilización para consumo humano, la calidad y el tiempo de almacenamiento de estas materias primas y su valor en el mercado. Con una inversión de US$ 53 424 para adaptar las bodegas al uso de AMR en una embarcación de 13,26 metros de eslora, cuya captura anual promedio es de 600 toneladas, los resultados del análisis financiero arrojan los siguientes valores:
|
Valor presente neto a i = 15% |
- US$ 25 440 |
|
Tasa interna de retorno |
- 47% |
|
Tiempo de repago |
- durante el 3er. año |
Tabla 7.10 Tasa de retorno sobre la inversión original (%) para las embarcaciones 1, 2 y 3
|
|
Inversión (US$) |
Base |
iROI 1 |
iROI 2 |
iROI 3 |
|
Embarcación 1 |
33 480 |
5,64 |
8,56 |
9,36 |
12,29 |
|
Embarcación 1 |
33 480 |
11,79 |
15,54 |
16,44 |
20,10 |
|
Embarcación 2 |
67 500 |
14,24 |
17,76 |
18,44 |
21,87 |
|
Embarcación 3 |
72 540 |
9,30 |
13,30 |
14,27 |
18,26 |
Además, se han efectuado estudios económicos sobre barcos destinados a la pesca de especies pelágicas, tal como anchoíta en el Perú. Para la determinación de la rentabilidad, se utilizó la variante del valor presente, conforme a la Ecuación (7.12) de este Manual, aplicando una tasa de descuento del 15%, basada en las tasas de interés de los préstamos que se otorgan, incluídos los gastos de administración y comisiones. En la Figura 7.8 se observa la variación de la rentabilidad con el tamaño de la bodega, para distintas tasas de interés. Con una tasa del 20%, los barcos menores de 200 toneladas no son rentables, mientras qué no existen beneficios para ningún barco si la tasa se eleva al 25% (Engstrom et al., 1974).
Figura 7.8 Influencia de la variación de la tasa de descuento
Se citan a continuación diversos análisis económicos correspondientes a diferentes plantas pesqueras pequeñas y medianas. Se realizó un análisis económico en pequeñas plantas de conservas de pescado de países tropicales, para producciones de 10 000 (modelo 1) y 20 000 (modelo 2) latas de 125 gramos de sardinas cada 8 horas. A su vez, se evaluó la sustitución de maquinaria (modelo 1) por mano de obra (modelo 3). La Tabla 7.11 muestra los valores correspondientes a la aplicación de los métodos de la tasa interna de retorno y del valor presente, considerando una tasa de descuento para el último método del 10%, que es el adoptado por el Tropical Products Institute en la evaluación de proyectos. Se ha tomado en cuenta una vida útil de 10 años.
Tabla 7.11 Evaluación de la rentabilidad para pequeñas plantas de conservas
|
|
Modelo 1 |
Modelo 2 |
Modelo 3 |
|
|
Valor presente (i=10%)(US$) |
1 262 100 |
2 678 910 |
1 153 382 |
|
|
Tasa interna de retorno ® |
61,5% |
69,5% |
59,0% |
|
|
A) |
200 días/año |
47,5 % |
54,0 % |
45,0 % |
|
150 días/año |
33,5 % |
38,5 % |
31,5 % |
|
|
B) 50% al mercado interno |
33,5 % |
39,0 % |
29,5 % |
|
|
C) +25% Costos de producción |
36,7 % |
42,6 % |
32,0 % |
|
También, se efectuó un análisis de sensitividad con los siguientes parámetros: (A) disminución de los días de trabajo por año (200 y 150); (B) 50% de la producción es vendida al mercado interno; (C) 25% de aumento en los costos de operación. El modelo base consideraba 250 días por año y el 100% de la producción se destinaba a la exportación, donde se obtienen precios más elevados que en el mercado interno (60%).
Las tasas internas de retorno ® disminuyen en promedio un 38,5 %. Si se consideran los dos primeros parámetros en conjunto, los valores encontrados son menores en un 50% y los resultados son negativos cuando se incorpora el tercer factor (Edwards et al., 1981).
La Tabla 7.12 muestra las inversiones requeridas y las TIR para plantas de conservas de pescados y mariscos en Indonesia (Bromiley et al., 1973).
Tabla 7.12 Tasas internas de retorno ® en plantas de conservas en Indonesia
|
Ubicación |
Capacidad anual (en '000 de latas) |
Inversión total (US$) |
r (%) |
|
Bitung |
104 (atún) |
1 850 000 |
36 (*) |
|
Pare-Pare |
720 (atún) |
360 000 |
35 |
|
Java central |
3 840 (camarón) |
810 000 |
45 |
Nota: (*) El cálculo de la tasa interna de retorno está afectado por los intereses que se deben abonar por la inversión; si se logra financiar la mitad de la inversión con un préstamo a 10 años con una tasa de interés del 12%, el valor de la tasa interna de retorno sería del 52%.
En Noruega, para plantas de conservas mecanizadas, con una capacidad de producción de 15 toneladas de materia prima por día (sardinas), se ha calculado una tasa interna de retorno del 27,1% (Myrseth, 1985). Existen evaluaciones donde es conveniente expresarlos resultados en función de algunas variables, cuya estimación es incierta. Por ejemplo, se estudió el comportamiento económico de plantas de congelado de pescado entero en bloques, para calcular a qué precio podría pagarse la materia prima, si se consideran favorables las tasas internas de retorno del 10 y 20% con vida útil de 15 años para las inversiones. Los resultados de estas evaluaciones se encuentran resumidos en la Tabla 7.13.
Se estudiaron dos niveles de producción. En el primer caso, se utilizaron 2 240 t de pescado entero, con dos turnos de 8 horas diarias, trabajando 250 días; en el segundo, se usaron 3 360 t con un turno adicional de 8 horas y un incremento en la capacidad de refrigeración y de la planta de hielo. Si los costos de energía disminuyen un 50%, el precio de compra de la materia prima podría aumentar en US$ 17/t. Se calculó una tasa interna de retorno para una hipotética planta de harina, con una inversión de US$ 10 000 (sobre un período de 5 años) al 18,5% (FAO, 1986a). En plantas pequeñas de ahumado de pescado, la distribución de las ganancias es similar al utilizado por los pescadores artesanales. Los ingresos recibidos de la operación de la planta se comparte igualmente entre los operarios de la planta, con una parte para la "asociación", una vez que los costos operativos han sido deducidos. Como la planta funciona con tres operarios, los ingresos son divididos en cuatro partes; una para cada operario y una para la Trade Union Association (FAO, 1986a).
Tabla 7.13 Precio resultante de materia prima para tasas internas de retorno del 10% y 20%
|
|
Precio materia prima (US$/t) |
||
|
r = 10% |
r = 20% |
||
|
Producción anual: 2 240 t |
|||
|
|
Inversión: US$ 322 430 |
109 |
94 |
|
Producción anual: 3 360 t |
|||
|
|
Inversión: US$ 535 480 |
380 |
243 |
En Sri Lanka, se evaluó la producción de ensilados líquidos para una planta de capacidad anual de 450 toneladas de producto considerando tres diferentes precios de venta, a partir de un valor de US$ 333/t y aplicando porcentajes de disminución del 20 y 25%. La determinación de las tasas internas de retorno para una vida útil de 5 años, dio como resultado los siguientes valores: 77, 38 y 26% respectivamente. Estos guarismos indican que el proyecto sería altamente rentable (Aagaard et al., 1980; Disney y James, 1980).
Otro análisis económico muestra la producción de ensilado líquido a partir de la fauna acompañante del camarón en México. La inversión fija asciende a US$ 28 289 y el capital de trabajo a US$ 6 667 para la producción anual de 312 toneladas de ensilado. Los costos de producción son de 92 US$/ton considerando un período de amortización de 5 años. El precio de venta se calculó adoptando una tasa interna de retorno del 15%, mostrando el ensilado ventajas significativas con respecto a los precios de otras fuentes de proteínas y de la harina de pescado. Cabe agregar que, el costo unitario por unidad de proteína es rentable, aún en el caso de utilizar en la producción especies e insumos (ácido) con precios más elevados (Edwards y Disney, 1980). En general, pareciera que la fabricación de ensilados líquidos es rentable, pero deben considerarse especialmente la distancia de la fábrica a los lugares de consumo y los precios competitivos de otros alimentos. No hay ninguna duda respecto a los beneficios de su utilización en las formulaciones de raciones para alimentar aves, peces de cultivo, pelíferos y pilíferos y cerdos (Bertullo, 1989; Andrade et al., 1992; Bello et al., 1992).
Para complementar los estudios de rentabilidad, es útil estudiar la influencia de ésta sobre cada componente de los ingresos, egresos e inversión. Conocer esta información permitirá ajustar fundamentalmente aquellos parámetros que demuestren la mayor influencia, dejando en una estimación menos ambiciosa los restantes.
En un análisis de sensitividad, se seleccionan algunas variables de diseño razonables y se varía cada una de ellas en etapas sucesivas, mediante algún porcentaje de variación permitido. Las variaciones resultantes en la rentabilidad revelan la importancia de cada variable investigada.
Ejemplo 7.10 Análisis de sensitividad
Realizar un análisis de sensitividad para una planta de conservas dadas las condiciones del caso base que se muestran en la Tabla 7.14. El parámetro relativo se define como la relación entre el valor real del parámetro y su valor en el caso base, calculándose de igual manera el cambio relativo de la tasa interna de retorno.
Tabla 7.14 Suposiciones del caso Base
|
1 |
La velocidad de producción es igual a las ventas anuales. |
|
2 |
Capacidad de la planta: 100 000 (latas/día). |
|
3 |
El capital de trabajo como función empírica de la inversión fija, los costos de operación y ventas. |
|
4 |
Depreciación por el método de la línea recta. |
|
5 |
Vida útil estimada: 10 años. |
|
6 |
Tasa impositiva: 45% (valor promedio para Argentina). |
|
7 |
Valor de reventa cero. |
|
8 |
Sin costos financieros. |
|
9 |
150 días/ano de producción (promedio para plantas de conservas en Argentina). |
|
10 |
El precio de venta se mantiene constante mientras los otros parámetros varían. |
Solución:
En la Tabla 7.15 y la Figura 7.9 se muestran los resultados obtenidos para el análisis de sensitividad.
Tabla 7.15 Análisis de sensitividad
|
Número en la Figura 7.5 |
Parámetro |
Variación del parámetro |
Valor relativo de la Tasa interna de retorno |
|
1 |
Precio de venta |
+ 10 |
1,90 |
|
- 4 |
0,57 |
||
|
2 |
Velocidad de producción |
+ 20 |
1,14 |
|
- 20 |
0,88 |
||
|
3 |
Precio de la materia prima |
+ 15 |
0,58 |
|
- 15 |
1,35 |
||
|
4 |
Precio de la lata |
+ 15 |
0,28 |
|
- 15 |
1,56 |
||
|
5 |
Inversión |
+ 20 |
0,64 |
|
- 20 |
1,20 |
||
|
6 |
Días por año |
+ 47 |
1,29 |
|
- 25 |
0,83 |
||
|
7 |
Costo de la mano de obra |
+ 20 |
0,63 |
|
- 20 |
1,31 |
Figura 7.9 Análisis de sensitividad para conservas de sardinas (Argentina, 1981)
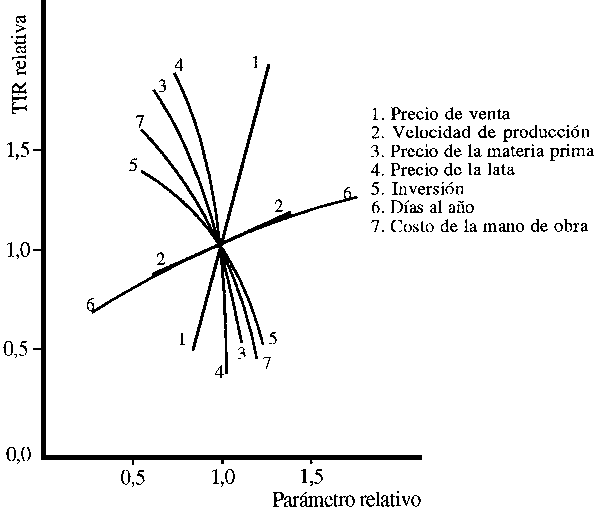
Se observa que pequeñas variaciones en el precio de venta y en los costos de materia prima (pescado y envases) modifican considerablemente la rentabilidad de la planta. Esto indicaría que en una estimación rápida de costos y rentabilidad, es necesario conocer esos datos con precisión, aún cuando no se conozcan con exactitud datos tales como la capacidad de planta, mano de obra, servicios, costos fijos, debiendo ajustarse extremadamente los cálculos de materia prima y realizando un estudio de mercado lo más exacto posible para determinar el precio de venta. Esto es particularmente cierto para procesos que no son de capital intensivo, esto es, aquellos controlados por los costos variables. Aquí el efecto del precio de venta sobre la rentabilidad es aproximadamente dos veces mayor que la de los otros parámetros (Cerbini y Zugarramurdi, 1981a).
7.9.1 Efecto de la inflación sobre el valor presente (VP)
7.9.2 Efecto de la inflación sobre la TIR. Tasa interna de retorno real
7.9.3 Efecto de la actualización del capital de trabajo sobre la TIR
7.9.4 Análisis continuo de la inflación
7.9.5 Efecto de la financiación del capital de trabajo sobre la TIR
7.9.6 Efecto de los préstamos para la inversión sobre la TIR
7.9.7 Efecto de los préstamos no indexados para la inversión sobre la TIR
7.9.8 Conclusiones generales sobre situaciones inflacionarias
Inflación es un fenómeno económico conocido y temido mundialmente; los países desarrollados lo monitorean de cerca y la inflación anticipada y la real aparecen en las noticias al menos una vez al mes. En muchos países en desarrollo los efectos de la inflación son soportados pacientemente. La inflación puede deberse a diferentes razones, usualmente ligadas a decisiones macroeconómicas y políticas, como emisión de moneda corriente sin el respaldo adecuado. En el Apéndice B.5 se puede encontrar información adicional sobre el concepto de inflación. En la Tabla 7.16 se indican series de tasas de inflación para varios países latinoamericanos, donde se puede observar la existencia permanente de valores muy altos (de 2 y 3 dígitos). Estas tasas de inflación tienen en cuenta una mezcla particular de bienes y servicios seleccionados para representar los deseos materiales de un ciudadano promedio.
Tabla 7.16 Costo de vida (Incremento promedio % anual)
|
Año |
Argentina |
Bolivia |
Brasil |
Colombia |
Chile |
México |
Uruguay |
|
1976 |
444,1 |
4,5 |
35,7 |
17,4 |
211,8 |
15,8 |
50,6 |
|
1977 |
176,0 |
8,1 |
40,5 |
28,6 |
91,9 |
28,9 |
58,1 |
|
1978 |
175,5 |
10,4 |
38,3 |
18,7 |
40,1 |
17,5 |
44,5 |
|
1979 |
159,5 |
19,7 |
50,2 |
24,2 |
33,4 |
18,2 |
66,8 |
|
1980 |
100,8 |
47,2 |
77,9 |
27,9 |
35,1 |
26,3 |
63,5 |
|
1981 |
104,5 |
32,2 |
95,6 |
29,4 |
19,7 |
28,0 |
34,1 |
|
1982 |
164,8 |
92,0 |
89,6 |
23,4 |
9,9 |
58,9 |
19,9 |
Fuente: (Index Económico, 1984): (Coyuntura and Desarrollo, 1983)
Dada la amplia base de cálculo, estos índices representan una tasa de inflación aplicable a distintos sectores de la economía. A este tipo de inflación se la denomina "general" y supone que todos los sectores de la economía (costos y precios) se inflacionan con una tasa uniforme. Por el contrario, la llamada "diferencial" o "reprimida" depende de cada insumo en particular. Por ejemplo, una compañía puede inflacionar sus costos de mano de obra o materia prima a diferentes tasas. Normalmente, la inflación es reprimida fundamentalmente debido a políticas oficiales en impuestos, control de importación, restricciones de precios, cambios tecnológicos o escasez de insumos. En procesos de inflación muy elevada, las variaciones "diferenciales" pierden importancia y pueden ser ignoradas, lo que se observa en la Tabla 7.17 en la que se incluyen series relativas a 1970 de diversos indicadores de inflación para la Argentina.
En la última fila b, de la Tabla 7.17, se observa que, aún tratándose de un período de profundos cambios sociales y económicos, las variaciones entre distintos sectores no superen el 10% con respecto a las variaciones de una inflación general.
A pesar que parece que en la mayoría de los países, incluyendo los países en desarrollo, se están moviendo ahora (1995) hacia condiciones más estables y menos inflacionarias, las empresas de procesamiento de pescado operan en el mundo real, y por lo tanto pueden necesitar sobrevivir bajo condiciones inflacionarias. La inflación afecta los cálculos de rentabilidad de los proyectos de inversión, causando que el análisis y la toma de decisiones se torne difícil y confuso. Esto es especialmente cierto en países donde las altas tasas de inflación son virtualmente constantes, como fue el caso de Argentina y otros países latinoamericanos.
Por ello, este análisis se limitará al caso de una inflación general pura sobre el análisis de rentabilidad de un proyecto, a efectos de diferenciar entre lo que es un beneficio real del que sólo puede calificarse como un resultado numérico, producto del proceso inflacionario.
Tabla 7.17 Indicadores de evolución de precios (base 1970 = 1) en Argentina
|
Año |
Indice de Costo de Vida |
Indice de costos de construcción |
Indice de Precios Mayoristas |
Indice de Precios Agropecuarios |
|||
|
Indice General |
Materiales |
Mano de Obra |
Gastos Generales |
||||
|
1970 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
1971 |
1,391 |
1,432 |
1,419 |
1,457 |
1,357 |
1,482 |
1,602 |
|
1972 |
2,284 |
2,268 |
2,393 |
2,158 |
2,253 |
2,608 |
3,002 |
|
1973 |
3,283 |
3,659 |
3,623 |
3,742 |
3,426 |
3,41 |
3,506 |
|
1974 |
4,598 |
5,98 |
6,343 |
5,816 |
5,283 |
4,642 |
4,259 |
|
1975 |
20,006 |
28,604 |
36,923 |
21,514 |
26,892 |
20,807 |
16,923 |
|
1976 |
89,536 |
91,00 |
136,27 |
50,836 |
88,822 |
101,18 |
94,593 |
|
1977 |
233,18 |
204,63 |
330,48 |
96,67 |
191,032 |
250,07 |
218,08 |
|
1978 |
629,22 |
517,14 |
810,69 |
262,81 |
475,890 |
608,43 |
557,60 |
|
1979 |
1 508,46 |
1 251,50 |
2 036,11 |
567,61 |
1 159,61 |
1 392,45 |
1 203,12 |
|
1980 |
2 830, 40 |
2 527,30 |
3 905,96 |
1 300,63 |
2 481,07 |
2 192,57 |
1 637,98 |
|
1981 |
6 545,96 |
5 247,30 |
8 320,66 |
2 611,65 |
4 768,25 |
6 143,51 |
5 123,00 |
|
1982 |
20 276,10 |
19 322,70 |
31 635,40 |
9 167,80 |
15 881,40 |
25 268,50 |
21 209,50 |
|
1983 |
108 208,90 |
127 361,00 |
181 936,00 |
79 248,90 |
104 299,00 |
129 013,00 |
103 829,60 |
|
b |
93,50 |
93,50 |
100,90 |
83,30 |
91,60 |
94,30 |
91,80 |
Nota: b: índice de inflación promedio (por mínimos cuadrados)
El uso de valores de flujo de caja en moneda constante aporta una solución para conocer valores de "tasa interna de retorno real". Si se quieren considerar algunos componentes del flujo de caja que son independientes de la tasa de inflación, tales como: la amortización de préstamos, actualización del capital de trabajo, se invalida la aplicación del flujo de caja en moneda constante para el cálculo de una TIR real y deben modificarse las fórmulas descriptas (de Santiago et al., 1987).
En primer lugar se analizará el efecto de la consideración de la inflación sobre los métodos de Valor presente y Tasa interna de retorno, aplicándolos al ejemplo de la planta de congelado.
La ecuación (7.11) es válida para el caso de inflación cero. En caso de tener inflación con una tasa fraccionaria b, esta ecuación puede describirse como:
Cuando b = 0 la ecuación (7.25) iguala la (7.11) con iR (tasa real) = i
Ejemplo 7.11 Cálculo del valor presente (VP) (considerando la inflación)
Calcular el valor presente (VP) para la planta de congelado de merluza del Ejemplo 7.1. Considerar una tasa de inflación del 80% anual, suponiendo que la planta está localizada en Argentina.
Solución: La conversión dólar es de 10000 Australes/US$ (1990), con lo cual la Tabla 7.1 expresada en Australes toma los valores de la Tabla 7.18.
Aplicando la Ecuación (7.11), el valor presente del proyecto al final del año 10 es 1 102 millones de Australes.
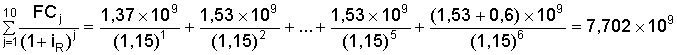
VP = (7,702 - 6,60) × 109 = 1,102 × 109; VP = 1 102 millones de Australes
Tabla 7.18 Cuadro de fuentes y usos para una planta pesquera cuando no existe inflación (en '000 millones de Australes (A))
|
Ejercicio |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
FUENTE |
|
|||||||||
|
Capital propio |
4,8 |
|
|
|
|
|
|
|
|
|
|
Crédito bancos (*) |
1,8 |
|
|
|
|
|
|
|
|
|
|
Ventas netas del ejercicio |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
|
Total (a) |
15,02 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
8,42 |
|
USOS |
|
|||||||||
|
Activo fijo |
6,0 |
|
|
|
|
|
|
|
|
|
|
Activo de trabajo |
0,6 |
|
|
|
|
|
|
|
|
|
|
Costos de financiación(**) |
0,27 |
|
|
|
|
|
|
|
|
|
|
Costos de producción |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
|
Total (b) |
13,74 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
6,87 |
|
Saldo (a) - (b) |
1,29 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
1,56 |
|
Beneficio neto (***) |
0,77 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
0,93 |
|
Más amortizaciones |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
0,60 |
|
Flujo de caja |
1,37 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
1,53 |
Notas:
(*) 30 % IF = A 1 800 000 000
(**) Tasa 15% anual
(***) descontando los impuestos a las ganancias (40%).
Ahora se puede modificar este ejemplo, suponiendo una tasa de inflación del 80% anual, pero suponiendo que ignoramos el efecto de la inflación y que se usa inapropiadamente la ecuación 7.11. Los datos para este caso son los mostrados en la Tabla 7.19, resultando un Valor Presente de 281,2 billones de Australes.
Tabla 7.19 Cuadro de fuentes y usos para una planta pesquera cuando hay inflación (b = 0,8) (en '000 millones de Australes (A))
|
Ejercicio |
1990 |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
|
FUENTE |
|
|||||||||
|
Capital propio |
4,8 |
|
|
|
|
|
|
|
|
|
|
Crédito bancos (*) |
1,8 |
|
|
|
|
|
|
|
|
|
|
Ventas netas del ejercicio |
15,2 |
27,3 |
49,1 |
88,4 |
159,2 |
286,5 |
515,7 |
928,3 |
1671,0 |
3007,8 |
|
Total (a) |
21,8 |
27,3 |
49,1 |
88,4 |
159,2 |
286,5 |
515,7 |
928,3 |
1671,0 |
3007,8 |
|
USOS |
|
|||||||||
|
Activo fijo |
6,0 |
|
|
|
|
|
|
|
|
|
|
Activo de trabajo |
0,6 |
|
|
|
|
|
|
|
|
|
|
Costos de financiación(**) |
0,5 |
|
|
|
|
|
|
|
|
|
|
Costos de producción |
12,4 |
22,3 |
40,1 |
72,1 |
129,8 |
233,6 |
420,5 |
756,9 |
1362,5 |
2452,5 |
|
Total (b) |
19,4 |
22,3 |
40,1 |
72,1 |
129,8 |
233,6 |
420,5 |
756,9 |
1362,5 |
2452,5 |
|
Saldo (a) - (b) |
2,3 |
5,0 |
9,1 |
16,3 |
29,4 |
52,9 |
95,2 |
171,4 |
308,5 |
555,3 |
|
Beneficio neto (***) |
1,4 |
3,0 |
5,4 |
9,8 |
17,6 |
31,7 |
57,1 |
102,8 |
185,1 |
333,2 |
|
Más amortizaciones |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
|
Flujo de caja |
2,0 |
3,6 |
6,0 |
10,4 |
18,2 |
32,3 |
57,7 |
103,4 |
185,7 |
333,8 |
|
Notas: |
(*) 30% de IF = A 1,800 000 000 |
|
|
(**) Tasa anual = 15% |
|
|
(***) descontando los impuestos a las ganancias (40%). |
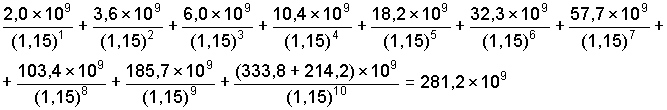
VP = (281,2 - 6,60) × 109 = 274,6 × 109; VP = 274 600 millones de Australes
Si la inflación se tiene en cuenta correctamente aplicando la ecuación 7.25, el resultado es netamente diferente, revela que el proyecto realmente tiene un valor presente negativo:
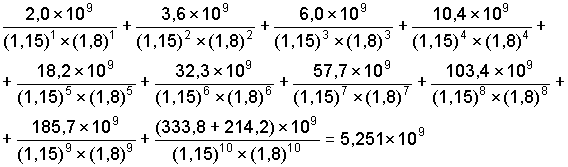
VP = (5,251 - 6,60) × 109 = - 1,349 × 109; VP = - 1 349 millones de Australes
El ejemplo propuesto permite observar que el efecto de la inflación es mostrar un proyecto más rentable de lo que realmente es.
La inflación afecta los cálculos de rentabilidad de proyectos de inversión, haciendo confuso su análisis y la toma de decisiones, muy especialmente en aquellos países en los que se alcanza permanentemente muy altas tasas de inflación. Al mismo tiempo, afecta negativamente las posibilidades de inversión.
Se utilizará el concepto conocido de tasa real que se basa en el siguiente razonamiento (Riggs, 1977; Barish y Kaplan, 1978): Considérese un depósito Io que al cabo de un año ha obtenido un interés Io × i:
I1 = Io × (1 + i) .......... (7.26)
Si en ese período hubo un inflación b, la relación entre el valor real de I1 (designado como I1o) y el valor de Io será:
I1o =I1/(l + b) = Io × (1 + i)/(1 + b) .......... (7.27)
Una tasa de interés real iR (descontando el efecto de la inflación) (Jelen y Black, 1983; Jones, 1982) puede ser definida por la expresión:
I1o = Io × (1 + iR) .......... (7.28)
Igualando (7.27) y (7.28) se deduce que:
Esta fórmula se diferencia de la comúnmente empleada:
iR~ (tasa de retorno real aproximada) = i - b .......... (7.30)
la que sólo es válida cuando b << 1, (Holland y Watson, 1977; Estes et al., 1980; Shashua y Goldschmidt, 1985) dando estimaciones de la tasa de interés real superiores a las definidas por la (7.29). Definiendo el error relativo cometido por la (7.31) encontramos que coincide con la tasa de inflación:
Introduciendo el concepto de tasa real de interés, definida por la (7.29) se determina una "tasa interna de retorno real" cuando se cumpla que la expresión (7.32) del flujo de caja descontado sea igual a cero:
donde FCj es flujo de caja neto en el año j y n es el número de períodos en la vida del proyecto. Si la economía es afectada por un fenómeno de inflación general, es de suponer que el numerador de cada uno de los términos de la sumatoria (flujo neto de caja del período j) se va expandiendo con la tasa de inflación.
FCj = FCj0 × (1 + b)j .......... (7.33)
Introduciendo la (7.33) en la (7.32) se observa que mediante el uso de valores de flujo de caja en moneda constante se conduce a valores de "tasa interna de retorno real" (TIR).
Ejemplo 7.12 Cálculo de la tasa interna de retorno, TIR ®
Calcular la tasa interna de retorno para la planta de congelado de merluza del Ejemplo 7.1. Considerar una tasa de inflación de 80%.
Solución:
De la Tabla 7.19, se obtiene un valor de r = 96,9%. Calculando la TIR a partir del flujo de caja neto corregido por inflación se obtiene una iR = 11%
De la ecuación (7.29):
Este resultado muestra nuevamente la incidencia de la inflación sobre un caso que parecía rentable cuando ésta no es tenida en cuenta. Además, como se ha dicho, en la práctica, diversos componentes del flujo de caja pueden ser independientes de la tasa de inflación, invalidándose así el uso de flujos de caja en moneda constante para el cálculo de una TIR real.
Se analizarán algunos de estos conceptos frente al problema de la inflación sobre un flujo de caja simple consistente en una inversión inicial que reditúa durante un período de vida de 10 años un flujo de caja constante si la tasa de inflación es cero.
La inflación obliga a un incremento del capital de trabajo IW. Para estudiar el efecto de este incremento sobre la rentabilidad se supondrá que el IW se puede expresar por una fracción fIW del monto anual de ventas "V". Considerando que las ventas anuales (V) y los costos operativos anuales (C) se expanden por la inflación es:
FCj = Vj - Cj = V0 × (1 + b)j - C0 × (1 + b)j .......... (7.34)
y habría una necesidad de incrementar anualmente el capital de trabajo por:
D IWj = fIW × Vj-1 × (1 + b) - fIW × Vj-1 = fIW × Vj-1 × b .......... (7.35)
recuperándose en el año N el capital acumulado
IWN = fIW × VN .......... (7.36)
Con ello la fórmula de la TIR (antes de impuestos) se transforma en:
Reordenando la expresión (7.37), se obtiene la expresión (7.38):
derivándose la siguiente expresión:
La ecuación (7.38) expresa el efecto de la inflación sobre la rentabilidad real ir por la desvalorización del capital de trabajo. A efectos de analizar dicha influencia se introducen en la (7.38) las siguientes relaciones adimensionales:
R=Vo/Co; X=Co/Io
y se divide por Io a toda la ecuación, que resulta así:
En la Tabla 7.20 se presenta un panorama de la influencia de los distintos parámetros que integran la expresión (7.40).
Tabla 7.20 Tasa interna de retorno real
|
BB* |
IW* |
b =0 |
0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
4,0 |
|
0,3 |
0,1 |
0,2447 |
0,2269 |
0,2089 |
0,1906 |
0,1794 |
0,1719 |
0,1567 |
|
0,3 |
0,2013 |
0,1554 |
0,1072 |
0,0559 |
0,0230 |
- |
- |
|
|
0,5 |
0,1703 |
0,1033 |
0,0310 |
- |
- |
- |
- |
|
|
0,7 |
0,1471 |
0,0661 |
- |
- |
- |
- |
- |
|
|
0,5 |
0,1 |
0,4440 |
0,4280 |
0,4120 |
0,3958 |
0,3861 |
0,3795 |
0,3665 |
|
0,3 |
0,3720 |
0,3306 |
0,2886 |
0,2456 |
0,2192 |
0,2013 |
0,1648 |
|
|
0,5 |
0,3191 |
0,2586 |
0,1960 |
0,1306 |
0,0893 |
0,0607 |
0,00002 |
|
|
0,7 |
0,2788 |
0,2032 |
0,1240 |
0,0390 |
- |
- |
- |
|
|
0,7 |
0,1 |
0,6320 |
0,6166 |
0,6011 |
0,5855 |
0,5762 |
0,5700 |
0,5575 |
|
0,3 |
0,5326 |
0,4930 |
0,4530 |
0,4127 |
0,3883 |
0,3720 |
0,3390 |
|
|
0,5 |
0,4595 |
0,4016 |
0,3429 |
0,2830 |
0,2462 |
0,2213 |
0,1703 |
|
|
0,7 |
0,4035 |
0,3313 |
0,2575 |
0,1810 |
0,1333 |
0,1004 |
0,0314 |
Nota:
N = 10
Se puede observar en la Tabla 7.20 que la tasa real de retorno se deteriora fuertemente con la inflación, y que el deterioro es más marcado a medida que el capital de trabajo tiene más importancia relativa. Para mantener la rentabilidad de la empresa, el recurso inmediato que dispone el empresario es aumentar el precio de venta de los productos en relación a los costos suponiendo que ello fuera posible sin disminuir el volumen de ventas.
Esta estrategia es representada por la ecuación (7.41) por R' > R y relacionándola con la misma expresión (7.41) con b = 0 y la R original, se puede obtener la proporción de aumento (R'/R) para mantener la rentabilidad iR constante, resultando la ecuación (7.41)
En la Figura 7.10 se representa la ecuación (7.41) para una tasa interna de retorno real "antes de impuestos", iR = 0,3. Se puede observar que la corrección necesaria puede llegar a valores muy altos, con lo que al aplicarse por todas las empresas provoca un aumento de los costos, generándose así un efecto multiplicador de la inflación.
Un análisis usando fórmulas contínuas, en el caso de la desvalorización del IW es pertinente por cuanto con altas tasas de inflación, los ajustes deben hacerse en períodos muy cortos. Para el caso contínuo se usarán las siguientes expresiones básicas, fácilmente deducibles:
|
Valor futuro: |
F(t) = F(o) × exp (i × t) |
.......... (7.42) |
|
Valor futuro en moneda constante: |
Fo (t) = F(o) × exp(i × t) exp(-b × t) |
.......... (7.43) |
|
Definición de tasa real de interés: |
Fo (t) = F(o) exp(iR × t) |
.......... (7.44) |
Obsérvese que en el caso continuo es válida la expresión aproximada (7.30). La ecuación continua de la TIR (caso sin inflación) es:
donde la i que hace cumplir la igualdad a cero es la tasa interna de retorno real. Para el caso con inflación se utilizarán las siguientes definiciones:
V = Vo × exp(b × t) .......... (7.46)C = Co × exp(b × t) .......... (7.47)
IW= fIW × V = fIW × Vo × exp(b × t) .......... (7.48)
y con ellas la ecuación que define la tasa interna de retorno real será:
Introduciendo el concepto de tasa de rentabilidad real (caso continuo iR = i - b) e integrando se obtiene:
Utilizando las relaciones X y R y dividiendo por Io la ecuación (7.51) se transforma en la (7.52), que es la expresión continua correspondiente a la (7.40).
y la expresión continua de (R'/R) correspondiente a la (7.41) es:
Las ecuaciones "continuas" (7.52) y (7.53) indican un efecto desfavorable mucho más marcado que sus similares discretas anuales al aumentar la tasa de inflación. Si bien las ecuaciones continuas constituyen un extremo inalcanzable, ellas indican que el análisis de períodos anuales puede conducir a errores graves en el análisis de rentabilidad. El análisis de la ecuación (7.53) indicaría que para altos fIW pasando ciertos valores de inflación, no existirían valores de R'/R que permitan mantener una rentabilidad razonable. Frente a ello, las empresas deben disminuir su capital de trabajo y aceptar rentabilidades menores. La persistencia del fenómeno de la inflación condeciría a la descapitalización de las empresas.
Algunos sectores productivos no tienen posibilidad de modificar el precio de venta de sus productos en el mercado, tal es el caso de las industrias que trabajan para la exportación, o en economías con libre competencia en el exterior. En ese caso, otro recurso disponible es el uso del crédito, que según el interés al que ha sido pactado puede mejorar o empeorar la rentabilidad del proyecto. Además reduce el monto de la inversión realizada por el empresario, lo que también altera la tasa interna de retorno.
Dada la gran variedad de tipos de préstamos, se analizarán solo algunos que permitirán hacer algunas generalizaciones. En primer lugar se analizará una financiación del capital de trabajo año a año. Así, en el período j se debe amortizar totalmente un préstamo:
fIW × Vo × (1 + b)j-1
pagando un interés iP y tomando un nuevo préstamo:
fIW × Vo × (1 + b)j
Para este caso la ecuación que define la TIR es la siguiente:
o en relaciones adimensionales:
A partir de la Ecuación (7.40), con b = 0 se obtiene la relación (7.55) que indica el iP máximo que podría pagarse por la financiación del capital de trabajo, manteniendo la rentabilidad iR constante e igual al caso de inflación cero.
iP = iR × (1 + b) .......... (7.56)
En la Tabla 7.21 se dan valores de iP calculados por la ecuación (7.56) para algunos casos utilizados en la Tabla 7.20. Se puede observar que sólo a bajas tasas de inflación, dependiendo de la rentabilidad del proyecto, es posible pagar intereses mayores que la tasa de inflación (tasas negativas). Aunque no sirva para mantener el nivel de rentabilidad, la financiación del capital de trabajo por préstamos a una tasa de inflación inferior a la rentabilidad global del proyecto (que incluye la inflación), produce una mejoría neta en la rentabilidad real, que no restituye la pérdida por inflación, si no se alcanzan los valores dados por la ecuación (7.56).
Tabla 7.21 Tasas de interés iP para financiar capital de trabajo que permitan mantener rentabilidad constante
|
BB* |
IW* |
iR = 0 |
b = 0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
|
0,3 |
0,7 |
0,1471 |
0,1765 |
0,2206 |
0,2942 |
0,3677 |
0,4413 |
|
0,5 |
0,1703 |
0,2043 |
0,2554 |
0,3406 |
0,4257 |
0,5109 |
|
|
0,3 |
0,2013 |
0,2418 |
0,3019 |
0,4026 |
0,5032 |
0,6039 |
|
|
0,1 |
0,2447 |
0,2436 |
0,3607 |
0,4894 |
0,6117 |
0,7341 |
|
|
0,5 |
0,7 |
0,2788 |
0,3345 |
0,4182 |
0,5576 |
0,6970 |
0,8364 |
|
0,5 |
0,3191 |
0,3829 |
0,4786 |
0,6382 |
0,7977 |
0,9573 |
|
|
0,3 |
0,3720 |
0,4464 |
0,5580 |
0,7440 |
0,9300 |
1,1160 |
|
|
0,1 |
0,4440 |
0,5328 |
0,6660 |
0,8880 |
1,1100 |
1,3320 |
En la Tabla 7.22 se indican las rentabilidades reales que alcanzarían financiando el capital de trabajo con tasa iP = b (tasas reales neutras) para los mismos casos de la Tabla 7.20, observándose importantes mejoras con respecto a los resultados consignados en la misma.
Tabla 7.22 Tasa de rentabilidad con financiación del capital de trabajo a tasas neutras
|
BB* |
IW* |
b = 0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
4,0 |
|
0,3 |
0,1 |
0,2538 |
0,2341 |
0,2141 |
0,2018 |
0,1936 |
0,1768 |
|
0,3 |
0,2141 |
0,1510 |
0,0814 |
0,0346 |
- |
- |
|
|
0,5 |
0,1726 |
0,0560 |
- |
- |
- |
- |
|
|
0,7 |
0,1287 |
- |
- |
- |
- |
- |
|
|
0,5 |
0,1 |
0,4733 |
0,4558 |
0,4381 |
0,4275 |
0,4204 |
0,4061 |
|
0,3 |
0,4381 |
0,3845 |
0,3298 |
0,2961 |
0,2732 |
0,2262 |
|
|
0,5 |
0,4025 |
0,3111 |
0,2141 |
0,1510 |
0,1056 |
0,0000 |
|
|
0,7 |
0,3664 |
0,2341 |
0,0814 |
- |
- |
- |
|
|
0,7 |
0,1 |
0,6795 |
0,6625 |
0,6455 |
0,6353 |
0,6285 |
0,6148 |
|
0,3 |
0,6455 |
0,5943 |
0,5428 |
0,5117 |
0,4908 |
0,4487 |
|
|
0,5 |
0,6114 |
0,5255 |
0,4381 |
0,3845 |
0,3482 |
0,2732 |
|
|
0,7 |
0,5772 |
0,4557 |
0,3298 |
0,2499 |
0,1936 |
0,0064 |
Se analizará a continuación la utilización de un préstamo sobre un porcentaje de la inversión, amortizable en cuotas iguales en moneda constante (préstamo con pagos indexados). Se supondrá que la amortización del préstamo es en N cuotas; siendo:
N: vida útil del proyectoMonto de préstamo: p × Io; 0 < p < l
Amortización: Aj = p × Io × FP (iP, N) × (1 + b)j
Con estos conceptos la tasa interna de retorno real es la que corresponde a la raíz de la ecuación adimensionalizada siguiente:
Como el interés pactado es equivalente a la tasa interna de retorno real de una inversión equivalente al monto prestado, es obvio que si el iP < iR, siendo iR la rentabilidad del proyecto sin el préstamo, para el inversor la rentabilidad mejoraría. Sin embargo, al aumentar la tasa de inflación y disminuir la rentabilidad por debajo del interés del préstamo, puede hacerse sumamente oneroso. En los resultados presentados en la Tabla 7.23, donde iR' es la rentabilidad del proyecto con préstamo a una tasa de interés iP = 0,1, se observa el efecto adverso cuando iR < 0,1.
Tabla 7.23 Variación de la tasa de retorno real con la inflación con préstamos indexados sobre la inversión. Tasa de interés del préstamo iP = 0,1
|
p = 0,7 |
b = 0 |
0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
4,0 |
|
Caso 1 | |||||||
|
BB* = 0,3 |
iR = 0,2013 |
0,1554 |
0,1072 |
0,0559 |
0,0230 |
- |
- |
|
IW* = 0,3 |
iR' = 0,2983 |
0,2083 |
0,1142 |
0,0130 |
-0,0530 |
- |
- |
|
Caso 2 | |||||||
|
BB* = 0,5 |
iR = 0,3191 |
0,2586 |
0,1960 |
0,1306 |
0,0893 |
0,0607 |
0,00002 |
|
IW* = 0,5 |
iR' = 0,4789 |
0,3723 |
0,2637 |
0,1518 |
0,0820 |
0,0338 |
-0,06780 |
|
Caso 3 | |||||||
|
BB* = 0,7 |
iR = 0,4035 |
0,3313 |
0,2575 |
0,1810 |
0,1333 |
0,1004 |
0,0314 |
|
IW* = 0,7 |
iR' = 0,5843 |
0,4663 |
0,3472 |
0,2259 |
0,1514 |
0,1006 |
-0,0045 |
En este caso la tasa de interés del préstamo debe ser menor que la tasa interna de retorno global (que incluye la tasa real más la tasa de inflación) para obtener una mejora en la rentabilidad. Ello se puede deducir del estudio de la siguiente ecuación adimensionalizada:
donde se ha considerado:
Monto de préstamo: p × Io ------- 0 < p < lAmortización: Aj = p × Io × FP (iP, N)
En la Tabla 7.24 se visualiza el hecho de que iR' > iR cuando i > iP. Este tipo de préstamo no ofrecería peligro frente a aumentos de la tasa de inflación.
Tabla 7.24 Variación de la tasa interna de retorno con préstamo no indexado en función de la inflación. Tasa de interés del préstamo iP =0,72; fracción financiada de la inversión p = 0,70
|
|
b = 0 |
0,2 |
0,5 |
1,0 |
1,5 |
2,0 |
4,0 |
|
Caso 1 |
iR = 0,2013 |
0,1554 |
0,1072 |
0,0559 |
0,0230 |
- |
- |
|
BB* = 0,3 |
i = 0,2013 |
0,3865 |
0,6608 |
1,1118 |
1,5575 |
- |
- |
|
IW** = 0,3 |
iR' = - |
0,01009 |
0,0938 |
0,1037 |
0,0908 |
- |
- |
|
Caso 2 |
iR = 0,3191 |
0,2586 |
0,1960 |
0,1306 |
0,0893 |
0,0607 |
0,00002 |
|
BB* = 0,5 |
i = 0,3191 |
0,5103 |
0,7940 |
1,2612 |
1,7232 |
2,1821 |
4,0001 |
|
IW** = 0,5 |
iR' = 0,0557 |
0,1774 |
0,2115 |
0,1914 |
0,1632 |
0,1388 |
0,07755 |
|
Caso 3 |
iR = 0,4035 |
0,3313 |
0,2575 |
0,1810 |
0,1333 |
0,1004 |
0,0314 |
|
BB* = 0,7 |
i = 0,4035 |
0,5976 |
0,8862 |
1,3620 |
1,8332 |
2,3012 |
4,157 |
|
IW** = 0,7 |
iR' = 0,1811 |
0,2891 |
0,2893 |
0,2468 |
0,2075 |
0,1764 |
0,1030 |
En el caso de altas tasas de inflación es preponderante el fenómeno de inflación general de todos los factores que se involucran en el flujo de caja descontado y el uso de valores en moneda constante conduce a una determinación de la tasa interna de retorno real. Sin embargo, la inflación produce una necesidad de continuos aportes al capital de trabajo, lo que ocasiona disminuciones de la rentabilidad, que pueden alcanzar valores relativos muy importantes.
Ello puede corregirse por aumentos en los márgenes de ventas siempre que ello sea posible, o por uso de préstamos. En este caso se ha mostrado que su efectividad se pierde al aumentar la tasa de inflación, pudiendo llegar a producir efectos adversos. En especial, los préstamos indexados (entre los que se considera los préstamos en monedas extranjeras cuya tasa de cambio sigue las tasas de inflación general) implican un alto riesgo pues en caso de aumentar la tasa de inflación originarían fuertes quebrantos.
Las fórmulas deducidas para flujos de caja con resultados repetidos en el tiempo, cuantifican estos conceptos, presentándose valores calculados en tablas en función de parámetros adimensionales que representan relaciones de ventas sobre costos operativos, costos operativos sobre inversión fija y capital de trabajo sobre ventas. Una generalización al caso continuo indicaría la necesidad de análisis en períodos cortos, pues el estudio en períodos anuales conduciría a errores altos en el caso de altas tasas de inflación.
La práctica comercial de aumentar el margen de ventas (para cubrir el costo de reposición) al generalizarse conduciría a una autoalimentación del proceso inflacionario, difícil de controlar por los mecanismos de la economía clásica.
La combinación de todos estos factores, con rendimientos variables año a año y tasas de inflación variables sólo puede resolverse por un flujo de caja descontado, incluyendo el concepto de rentabilidad real definida por la (7.32), pero las fórmulas presentadas en función de parámetros adimensionales, dan una idea general muy útil en la toma de decisiones sobre estrategias a seguir en caso de tasas de inflación elevadas.
Tasas altas de inflación, o tan sólo inflación, no es una situación deseada por una empresa, pero es una situación para enfrentar a fin de sobrevivir. De la experiencia en países con alta inflación, se ve claramente que la mayoría de los esfuerzos gerenciales en tales situaciones, se dirigen hacia el desarrollo de estrategias financieras a fin de sobrevivir. Otros aspectos, como desarrollo del mercado, tecnología y calidad, reciben menor o ninguna atención. Desafortunadamente, las altas tasas relativas de inflación continúan siendo un problema en muchos países en desarrollo. Por ello, se encontró necesario incluir este análisis -ciertamente no restringido a la industria pesquera- para proveer herramientas apropiadas para el lector interesado.