9.1 Derivación de la ecuación del rendimiento
9.2 Otras formas de la ecuación del rendimiento
9.3 Ejercicios
Las secciones anteriores están dedicadas a los métodos de recoger los datos básicos, analizarlos y obtener estimaciones de los parámetros de la población - crecimiento, mortalidad, edad de reclutamiento, etc. -. En esta sección y en las posteriores se tratará de cómo usar estas estimaciones para explicar y comprender la historia anterior de la pesquería, y predecir su futuro; en particular, para predecir el efecto de los cambios en el régimen de pesca debidos a cualquier medida propuesta de regulación o conservación.
El cálculo más sencillo es cuando se trata de una población en la cual los diferentes parámetros son constantes Para una población así, es mejor hacer los cálculos del rendimiento de una sola clase anual de peces durante su vida, el cual será, en régimen permanente, el mismo que el rendimiento en un año de todas las clases de edad presentes en la pesquería. Se puede dividir la totalidad de la vida en períodos relativamente cortos; para cada período, puede calcularse el numero de peces vivos, el número capturado, el número que muere por causas naturales (no debidas a la pesquería) y el número de supervivientes al comienzo del período siguiente, y finalmente el rendimiento, en peso que se calculará multiplicando el número de individuos capturados por su peso medio. Este proceso puede hacerse aritméticamente, pero para obtener mayor precisión, los períodos escogidos deben ser cortos y por lo tanto, numerosos, y los cálculos pueden llegar a ser muy laboriosos. Es más fácil expresar el rendimiento en una forma algebraica, la cual tiene la gran ventaja de mostrar explícitamente la influencia de los diferentes parámetros en el rendimiento.
Definiremos los términos como sigue:
Nt = número de peces vivos a la edad t.R = número de reclutas, es decir, número de peces vivos a la edad tr.
R' = número de peces vivos a la edad tc, a la cual comienzan a ser retenidos por el arte en uso.
M = coeficiente instantáneo de mortalidad natural.
F = coeficiente instantáneo de mortalidad por pesca.
Entonces, para tr < t < tc:
es decir que la tasa instantánea a la que mueren los peces por causas naturales es igual al producto del coeficiente de mortalidad natural por el número de peces. Integrando:
porque N = R cuando t = tr
-M (t0 - tz)
y R' = Re
y para t > tc, cuando están operando tanto la mortalidad natural como por pesca:
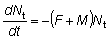
y
(9.1)
o también
El número de peces capturados en el intervalo de tiempo (t, t + dt), será FNtdt, de manera que el número total capturado, C, se obtendrá dividiendo el período total de tiempo entre tc (la edad de primera captura) y tL (la edad máxima alcanzada) en intervalos cortos, y añadiendo las contribuciones de cada intervalo.
Matemáticamente, esto se expresa mediante la integral (véase la Sección 2).
por lo tanto
o integrando
(9.2)
la cual, si se considera tL lo suficientemente grande para
poder despreciar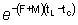 
se reduce
a:
(9,2')
Así pues, la pesca toma una parte del número total de individuos que alcanzan la edad de primera captura igual a la razón entre la mortalidad por pesca y la mortalidad total.
De la misma forma, el peso capturado en el intervalo de tiempo (t, t + dt) viene dado por:
dYt = FNtWtdt
donde Wt es el peso medio de un pez de edad t.
El peso total capturado vendrá dado por lo tanto, por
(9,3)
Para poder integrar fácilmente esta ecuación, la expresión para el peso debe estar en una forma apropiada; de las ecuaciones de crecimiento discutidas anteriormente, la de VON BERTALANFFY es una de las más convenientes. Entonces podemos escribir:
o, escribiendo el miembro de la derecha como una sumatoria:
donde
U0 = 1, U1 = -3, U2 = 3, U3 = -1
Entonces,
o también, escribiendo t - t0 = (t - tc) - (tc - t0) y redistribuyendo los términos
e integrando
(9.4)
De nuevo, esta expresión puede simplificarse si tL es lo suficientemente grande para poder despreciar el último término. Entonces el rendimiento viene dado por:
o también, sustituyendo R'
(9.5)
Además del rendimiento total, hay algunas otras cantidades que son importantes. Por ejemplo, el rendimiento es F multiplicado por la bio-masa media total de los peces en fase explotada, B', y por lo tanto
(9.6)
Análogamente, el número medio en la fase explotada es, dividiendo en la ecuación (9.2') la captura en número por F:
El peso medio de los peces individuales en la fase explotada es, por tanto:
Como el reclutamiento es desconocido y a menudo variable, los rendimientos, etc., se calculan normalmente como rendimiento, etc., por recluta.
Las operaciones necesarias para calcular el rendimiento directamente de la ecuación (8.5), han sido expuestas en las plantillas de trabajo adjuntas. La primera, (A), muestra una ordenación para calcular el rendimiento para una serie de valores de la mortalidad por pesca, (F), siendo constante la selectividad, (tc). Las entradas en la casilla del extremo superior izquierdo se completarán con los conocimientos que se tengan de los diferentes parámetros de la población, sea usando las mejores estimaciones disponibles o, si el conocimiento de los mismos no es tan preciso, una serie de valores para la mortalidad natural, etc.; se usa una planilla separada para cada conjunto de valores posibles. Las entradas en la parte superior central contienen los cálculos que son iguales para todos los valores de F. Debajo hay cuatro pares de columnas (B) y (C) correspondientes a los cuatro términos de la suma de la ecuación (8.5). (Para mayor facilidad, la mayoría de las entradas, columnas, etc., han sido designadas por letras puestas entre paréntesis, para evitar confusión con las letras usadas en las ecuaciones para los coeficientes de mortalidad, etc.). En la segunda línea de cada columna se indica la fórmula que será utilizada normalmente para computar la entrada de esa columna (ejemplo, en la columna (Q) - (P) x (N)) y la tercera línea muestra lo que la entrada representa en función de los diferentes parámetros (ejemplo, en la columna (Q) - B'/R).
Las otras planillas (B1) y (B11) son usadas para calcular el rendimiento para varias selectividades. La primera (Bi) se usa para calcular tc (y otras cantidades relacionadas) a partir de la selectividad, la cual normalmente será definida por el tamaño a la primera captura, lc. En la planilla (Bii) que es casi igual a la (A), puede ser calculado el rendimiento para diferentes selectividades y determinadas mortalidades por pesca.
Es posible reducir los cálculos y también tener en cuenta una relación longitud/peso distinta de la cúbica expresando el rendimiento Y en otra forma, utilizando la función Beta incompleta.
Esta función, que se acostumbra designar por Bx (p, q) es definida por la integral
donde p, q, son constantes positivas, y el límite superior de la integración x está comprendido entre 0 y 1. Para x = 1, la función es llamada Beta completa y designada por B (p, q)
Para obtener la expresión del rendimiento Y como una función Beta, partamos de la ecuación (9.3) con tL = ¥, o sea,
en lo que
la cual, observando que t - tc = (t - t0) - (tc - t0), puede escribirse:
o, si W¥ es proporcional a lb
Haciendo la sustitución de la variable de integración t por y según la transformación
y calculando los límites de la integración para la nueva variable,
t = ¥ se convierte en y = 0
y t = tc resulta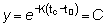 
Asimismo, la expresión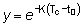 
,
que es igual a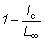 
, será
designada por 1 - c y los diferentes factores de la integral se transforman
entonces en:
El rendimiento en peso Y se transformará entonces en
o escribiendo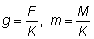 
Expresando la integral como una función Beta incompleta se tiene:
o, si b = 3
(9.7)
Esta expresión del rendimiento puede considerarse en dos partes: la
primera 
no contiene ninguno
de los parámetros (F o tc) que dependen de la
intensidad o régimen de pesca. Esta parte puede, por tanto, considerarse
como constante al estudiar el efecto sobre el rendimiento de distintos regímenes
de pesca. La segunda parte contiene solamente cuatro parámetros, las
relaciones m = M/K, g = F/K y b y c.
Existen tablas de la función Beta incompleta (JONES, 1957; WILIMOVSKY y WICKLUND, 1963). HOLT (1957) ha preparado tablas de g (1 - c)g. En consecuencia, el rendimiento puede ser expresado como el producto de una constante y de dos cantidades obtenibles en las tablas.
Debe observarse que
es decir, que es la proporción del crecimiento total en longitud a que ha llegado el pez antes de que entre en la fase explotada. A pesar de la aparente complejidad de la expresión correspondiente al rendimiento, ésta se determina mediante unas pocas cantidades solamente: la proporción del desarrollo logrado cuando el pez es reclutado, y las magnitudes relativas de la mortalidad por pesca, de la mortalidad natural y del parámetro K de crecimiento.
Como, en realidad, b raramente difiere mucho de 3, normalmente se puede
utilizar la ecuación 9.7. Aparte un término constante, al comienzo,
ésta tiene solamente tres variables independientes, C, g
y m, y fácilmente se puede tabular directamente una función
de tres variables. Así lo han hecho BEVERTON y HOLT (1964), explícitamente
como una función de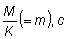 
y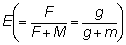 
. Los mencionados autores
dedujeron la fórmula de una forma algo diferente, pero es una cuestión
de matemática sencilla formular su expresión (12) para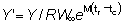 
en función de c, m y g, es decir:
que puede demostrarse que es igual a g (1 - c)-gB1-c (m + g, 4).
Se han tabulado estas tablas de rendimientos para una serie de valores de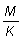 
desde
0,25 hasta 5,00. Para cada valor de ,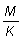
el cuadro de valores de Y' (proporcional al rendimiento por recluta)
forma el equivalente de un diagrama de isopletas de rendimiento del cual puede
ser determinada con mucha facilidad la forma de la relación entre el
rendimiento y la intensidad de pesca o el tamaño en la primera captura.
Habrá de tenerse algún cuidado al interpretar las variaciones
en la intensidad de pesca, ya que las tabulaciones se dan en función
de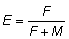 
, y para valores grandes
de E - de más de 0,5 - los cambios muy pequeños
de E corresponden a grandes cambios de F.
Pueden obtenerse otras formas que dan el rendimiento sustituyendo el peso en la ecuación (9.3) por diferentes fórmulas. En particular, a lo largo de un período de tiempo relativamente corto, como por ejemplo, de t1 a t2, el crecimiento en peso puede considerarse como exponencial; esto es,
donde W1 es el peso en el instante t1.
El coeficiente de crecimiento g1 cambiará de acuerdo con el intervalo escogido, disminuyendo generalmente al aumentar la edad. Sustituyendo, el rendimiento en peso durante el período t1 - t2 será:
.
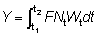
El rendimiento total puede entonces obtenerse sumando los valores correspondientes a la totalidad de la vida, utilizando un número suficiente de intervalos. La ventaja de expresar el crecimiento en esta forma es que el tamaño (o la edad) al cual la masa total de una clase anual alcanza su máximo, es el tamaño en el cual g es igual al coeficiente de mortalidad natural M (el «tamaño crítico» de RICKER). El rendimiento máximo se obtiene por lo tanto capturando todas las clases anuales tan pronto como alcanzan este tamaño. Cuando no se cumplen los supuestos de la ecuación simple de rendimiento (por ejemplo, distinta modalidad de crecimiento, parámetros no constantes, etc.), existe siempre la posibilidad de aplicar el método mencionado en el segundo párrafo de esta sección, expresando el rendimiento como la suma de los rendimientos en un gran número de intervalos muy breves, dentro de los cuales los cambios en el tamaño de los individuos y en el número de individuos de la población pueden despreciarse. Es decir, que nos aproximamos a la integral de la ecuación 9.3 con la expresión
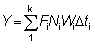
(véase Sección 2)
en donde el intervalo de tiempo de tc a tL ha sido dividido en k intervalos cortos, y en la que
Fi = mortalidad por pesca en el i-ésimo período.
Ni = número de individuos presentes al principio del i-ésimo período
Wi = peso medio de los individuos durante el i-ésimo período
y D t1 = duración del i-ésimo período.
Fi puede ser considerada como constante = F, o se pueden utilizar algunos valores empíricos si existe evidencia de que la mortalidad por pesca varía con la edad. Análogamente, Wi puede ser determinado a base de una curva de crecimiento adecuada, o bien se pueden utilizar en este caso también datos empíricos para tener en cuenta factores tales como las variaciones estacionales en el crecimiento, etc.
Ni puede ser determinado sirviéndose de la fórmula usual
en la que
o de las ecuaciones
N1=R'Ni+1 = Ni - (Fi + M)NiD ti
La expresión del rendimiento en esta forma es probable que sea particularmente valiosa en cualquier pesquería en la que no se cumplen con toda exactitud los supuestos de la curva de rendimiento simple; por ejemplo, pesquerías muy estacionales, o pesquerías como las de redes de enmalle, en las que la mortalidad por pesca puede variar con la edad. Se han llevado a cabo estudios detallados mediante calculadoras electrónicas respecto a las pesquerías de salmón del Pacífico donde existen regulaciones complicadas que comprenden distintos artes de pesca, así como un gran número de poblaciones que se mezclan en mayor o menor grado.
A. Efectos de un cambio en la intensidad de pesca
A1. Solla del Mar del Norte (malla de 75 mm).
Los valores aproximados de los parámetros para la solla del Mar del Norte con malla de 75 mm., son los siguientes:
M = 0,1
L¥ = 68,5 cm.
W¥ = 2.860 g.
K = 0,095
t0 = -0,8 años.
tr = 3,7 años.
tc = 3,7 años.
(Téngase en cuenta que la solla del Mar del Norte no se desplaza hasta los caladeros principales hasta que llega a los 3 o 4 años de edad, de modo que su talla a la primera captura es independiente del tamaño de la malla cuando se trata de mallas de hasta unos 100 mm.).
(a) Usando la planilla A, calcular y representar prácticamente frente al coeficiente de mortalidad por pesca (F), las curvas de peso de la población explotada por recluta (P'/R) (proporcional a la captura por unidad de esfuerzo).
Rendimiento por recluta (Y/R). Exprésese en gramos y también como porcentaje del rendimiento actual (es decir, con F = 0,5).
Número de individuos de la población explotada por recluta. (N'/R).
Captura en número por recluta (C/R).
Peso medio de los peces en la captura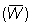 
.
Nota: Tómese F = 0; 0,02; 0,04; 0,06; 0,08; 0,1; 0,2; 0,5; 1,0.
(b) De las tablas de funciones del rendimiento (Parte II de este Manual),
y utilizando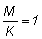
, expresar el
rendimiento por recluta para cada valor de E en las tablas como porcentaje
del rendimiento por recluta al valor actual de E (considerando este
como 0,8). Represéntese gráficamente este valor (1) frente a E,
y el de (2) frente a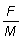 
. (Nota:
calcúlese primero c). ¿Qué relación guarda la curva
b2 con la curva de rendimiento por recluta en función del esfuerzo obtenido
en (a)?
(c) La estimación actual de F para la solla del Mar del Norte es de alrededor de 0,5. ¿Qué porcentaje de cambio en la intensidad de pesca con respecto al nivel presente se necesita para obtener el máximo en el rendimiento constante por recluta? ¿En qué porcentaje difiere este rendimiento del nivel actual? ¿Qué efecto tendría este cambio en la intensidad, sobre la captura por unidad de esfuerzo y el peso medio de los peces en la captura? ¿En qué forma dependen estas respuestas de la magnitud de M?
Repítase lo anterior para una malla de 140 mm., considerando que tc, para este tamaño de malla, es igual a 5,5 años.
A2. Eglefino del Mar del Norte (malla de 75 mm.).
Los valores aproximados de los parámetros, para una malla de 75 mm., son los siguientes:
M = 0,2
L¥ = 55 cm.
W¥ = 1.300 g.
K = 0,25
t0 = -0,2 años.
tr = 1,0 años.
tc = 2,1 años.
(a) Llevar a cabo el ejercicio Al, tal como se detalló anteriormente.
(Nota: la estimación actual de F para el eglefino del Mar del
Norte es de alrededor de 0,8; en las tablas de rendimiento utilícese
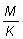= 0,50 y 1,25).
(b) Repítase el ejercicio con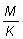
= 0,50 y 1,25.
(c) Repítase el ejercicio anterior para una malla de 100 mm., considerando tc = 3,3 años.
B. Efectos del cambio en el tamaño de la malla
B1. Solla del Marte del Norte (F = 0,5).
(a) Para tamaños de malla mayores de 120 mm., la longitud media de selección lc puede ser calculada directamente del factor de selección b = 2,2. Usando las planillas B1 y B2, con F = 0,5, calcular y representar gráficamente en relación con el tamaño de la malla, las curvas e B'/R, V/R, C/R, y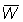 
. Tómese M = 0,1 y los otros valores de los parámetros indicados en A1. Expresar el rendimiento como porcentaje del rendimiento actual, es decir, con una malla de 75 mm. (Nota: tómense de malla de 120, 160, 180, 200, 220, 240 y 260 mm. y trácense también los valores para las mallas de 75 y 140 m. precedentemente calculados para F = 0,5).
(b) Utilícense las tablas de rendimiento correspondiente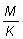
= 1,0 para determinar la forma de la curva de rendimiento por recluta en función
del tamaño de la malla. Repítase el ejercicio para valores de
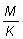= 0,5 y 1,5. (Primero calcúlese
E y utilícese el valor más aproximado de E en las
tablas).
(c) ¿Qué tamaño de malla es preciso usar para obtener el rendimiento estable máximo por recluta con este valor de F? ¿En qué porcentaje difiere este rendimiento del rendimiento actual? ¿Cuáles serían los cambios correspondientes en la captura por unidad de esfuerzo y en el peso medio de los peces en la captura? ¿En qué grado dependen estas respuestas del valor de M?
(d) Repítanse los ejercicios (a) - (c) como en B1, pero usando un valor F = 0,2 en ellos. Compárense los últimos resultados y conclusiones con los obtenidos con F = 0,5.
B2. Eglefino del Mar del Norte (F = 0,8).
(a) La relación entre el tamaño medio de selección lc y el tamaño de la malla para el eglefino puede ser calculado con un factor de selección de 3,2. Utilizando las planillas B1 y B2 siendo F igual a 0,8.
Calcular y representar gráficamente en función del tamaño de la malla las curvas P'/R, Y/R, N'/R, C/R, y W. Tómense los valores de los parámetros indicados en A2. (Nota: Tómense tamaños de malla de 80, 90, 120, 150 y 160 mm. Trácense igualmente los valores para las mallas de 75 y 100 mm., precedentemente calculados para F = 0,8).
(b) Utilícense las tablas de rendimiento para determinar la forma de
la curva de rendimiento por recluta en función del tamaño de la
malla para 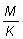0,50, 0,75 y 1,25
(utilícese E = 0,85, 0,80, y 0,70).
(c) ¿Qué tamaño de malla es preciso usar para obtener el rendimiento estable máximo por recluta con este valor de F? ¿En qué porcentaje difiere este rendimiento del nivel actual? ¿Cuáles serían los cambios correspondientes en la captura por unidad de esfuerzo y en el peso medio de los peces en la captura? ¿En qué grado dependen estas respuestas del valor de M?
(c) Repítanse los ejercicios (a) - (c), como en B2, pero usando F = 0,3 en ellos.
(d) Compárense los últimos resultados y las conclusiones con los obtenidos con F = 0,8, y también con los obtenidos para la solla del Mar del Norte.
PLANILLA (A)
EVALUACION DE LA INTENSIDAD DE PESCA
|
Datos | |
|
Especie |
|
|
Malla |
|
|
M |
|
|
W¥ |
(gm) |
|
K |
|
|
t0 |
(años) |
|
tc |
(años) |
|
tr |
(años) |
tc - tr =
M (tc - tr) =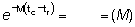
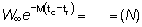
tc - t0 =
K (tc - t0) =
|
|
|
|
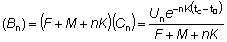
(Gn) |
|
n |
(D)n |
Un |
Un (D)n |
|
0 |
1 |
+1 |
+1 |
|
1 |
|
-3 |
|
|
2 |
|
+3 |
|
|
3 |
|
-1 |
|
|
|
n = 0 |
n = 1 |
n = 2 |
n = 3 |
| |||||||||
|
(A) |
(B0) |
(C0) |
(B1) |
(C1) |
(B2) |
(C2) |
(B3) |
(C3) |
(P) |
(Q) |
(R) |
(S) |
(T) |
(V) |
|
F |
(A) + M |
1/(B0) |
(A) + M + K |
(G1)/(B1) |
(A) + M + 2K |
(G2)/(B2) |
(A) + M + 3K |
(G3)/(B3) |
(C0) + (C1) + (C2) + (C3) |
(P) x (N) |
(Q) x (A) |
(C0) x (M) |
(S) x (A) |
(Q)/(S) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B1/R |
Y/R |
N'/R |
C/R |
|
PLANILLA B (L)
EVALUACION DEL TAMAÑO DE MALLA (1)
|
Datos | |
|
Especie |
|
|
W¥ = |
(gm) |
|
F = |
|
|
M = |
|
|
L¥ = |
(cm) |
|
K = |
|
|
tc = |
(años) |
|
tr = |
(años) |
|
b = |
|
Nota
|
(A) |
(B) |
(C) |
(D1) |
(D2) |
(D3) |
(G) |
(H) |
(J) |
(K) |
(L) |
(M) |
(N) |
|
Malla (cm.) |
(A) x b |
(B)/L¥ |
1 - (C) |
(D1)2 |
(D1)3 |
-loge (D1) |
(G)/K |
(H) + tc |
(J) - tr |
(K) x M |
e-(L) |
(M) x W¥ |
|
|
lc |
lc/L¥ |
|
|
|
K (tc - t0) |
tc - t0 |
tc |
tc - tr |
M (tc - tc) |
|
|
PLANILLA B (2)
EVALUACION DEL TAMAÑO DE MALLA (2)
|
Datos | |
|
Especie |
|
|
F = |
|
|
M = |
|
|
W¥ = |
(gm) |
|
K = |
|
|
t0 = |
(años) |
|
tr = |
(años) |
|
b = |
|
Nota
|
|
(Fn) |
|
n |
F + M + nK |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
|
n = 0 |
n = 1 |
n = 2 |
n = 3 |
| ||||||||||
|
(A) |
(E0) |
(C0) |
(E1) |
(C1) |
(E2) |
(C2) |
(E3) |
(C3) |
(P) |
(Q) |
(R) |
(S) |
(T) |
(V) | |
|
Malla (cm.) |
(D0) |
(E0)/ (F0) |
-3(D1) |
(E)/(F1) |
3(D2) |
(E2)/ (F1) |
(D3) |
(E3)/(F3) |
(C0) + (C1) + (C2) + (C3) |
(P) x (N) |
(Q) x F |
(C0) x (M) |
(S) x F |
(Q)'(S) | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
P'/R |
Y/R |
N'/R |
C/R |
| |
