10. EVALUACIONES ESPECIALES

10.1 Estadísticas de captura y esfuerzo
10.2 Modelo de Schaefer
10.3 Cambios en la selectividad
10.4 Pesquerías que actúan recíprocamente
10.5 Ejercicios

La ecuación simple de rendimiento descrita en la sección anterior depende, para su cálculo, de un conocimiento bastante completo de los diferentes parámetros (crecimiento, mortalidad, etc.) y con esta información, es posible estimar el rendimiento estable para cualquier combinación de mortalidad por pesca y edad de primera captura. Sin embargo, incluso en el caso de que, como a menudo sucede, la información no es del todo completa, es posible dar respuesta a algunas cuestiones específicas, como por ejemplo, ¿aumentaría o disminuiría el rendimiento estable por un aumento moderado del tamaño a la primera captura?

10.1 Estadísticas de captura y esfuerzo

Si hay estadísticas disponibles para un cierto número de períodos en los cuales el esfuerzo fue mantenido a un nivel estable, es claro que será posible derivar una relación puramente empírica entre el esfuerzo de pesca y el rendimiento constante, o la captura por unidad de esfuerzo. En la mayoría de las pesquerías hay pocos períodos "largos de esfuerzo de pesca constante, si es que hay alguno, y tanto la captura como la captura por unidad de esfuerzo en cualquier año estarán relacionados no solamente con el esfuerzo en ese año, sino con el esfuerzo en los años precedentes. Sin embargo, la abundancia de una determinada clase anual que ha estado en la pesquería, digamos, cuatro años (es decir, que es de edad t_c + 4) estará determinada por un factor igual a 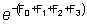donde F₀, F₁, F₂, F₃, son las mortalidades por pesca en los cuatro años anteriores; es decir, que su abundancia será la misma que si hubiera estado en una pesquería con una mortalidad por pesca constante de 1/4 (F₀ + F₁ + F₂ +F₃). La captura total por unidad de esfuerzo (c.p.u.e.) de todas las edades está relacionada con una media ponderada de los esfuerzos de pesca en los años anteriores. Si esta media se toma durante un período igual a la duración media de la vida en la fase explotada (por ejemplo, si la edad en el reclutamiento es de 4 años, y la parte principal de la captura en peso, está compuesta de individuos entre 4 y 9 años, la duración media es de alrededor de 3 años), entonces la relación entre este esfuerzo medio 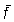y la captura será aproximada a la que existe entre el esfuerzo y la c.p.u.e. en régimen constante. La concordancia será casi exacta, no solamente cuando el esfuerzo no se ha alterado grandemente, sino también cuando ha habido una tendencia uniforme en el esfuerzo. Por ejemplo, si el esfuerzo ha ido en aumento, entonces habrá una superabundancia de las edades mayores que habrán sufrido un esfuerzo de pesca medio menor que 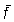, mientras que las edades más jóvenes serán muy escasas, habiendo experimentado un esfuerzo medio mayor que .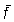

Esta relación se expresa mejor gráficamente, trazando la c.p.u.e. en función de 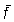; la línea de mejor ajuste generalmente no será una recta, sino una curva cóncava hacia arriba (por ejemplo, las curvas correspondientes a la solla y el bacalao en Islancia (GULLAND, 1960)). De esta curva supuesta una relación en régimen constante entre la c.p.u.e. y el esfuerzo, puede ser determinada inmediatamente por multiplicación la relación correspondiente entre captura y esfuerzo.

Este método está muy próximo al modelo de parámetros constantes de la curva completa de rendimiento, en el cual se ignoran los efectos dependientes de la densidad, debido a que la mayoría de los mismos actúan durante períodos más largos de tiempo. Por ejemplo, en el caso anterior, si el reclutamiento resulta afectado, la población actual es la que proviene de una población del promedio de seis o siete años antes, la cual, a su vez fue determinada por la pesca en los tres o más años anteriores.

La principal ventaja de este método es que requiere datos fáciles de obtener; la captura total usualmente es conocida, y los datos de esfuerzo o de c.p.u.e. están entre los primeros datos semi-científicos que son escogidos. Si hay errores en los datos de esfuerzo (los más probables son tendencias sin corregir, como puede ser el aumento de la eficiencia), éstos afectarán los valores de x e y en el gráfico y tenderán a desplazar los puntos a lo largo de las líneas de la fórmula y = a/x. El desplazamiento se producirá en una dirección similar a la forma general de la regresión esperada, de manera que, al parecer, los errores en la medida del esfuerzo no distorsionarán la estimación de la relación entre la c.p.u.e. y el esfuerzo, pero harán que la significación estadística del ajuste sea mayor de lo que realmente es. Si la serie de datos es lo suficientemente larga, el efecto de los cambios que no sean simplemente del esfuerzo total, puede ser estudiado. Así, por ejemplo, si en el medio de la serie ha habido un cambio en el método de pesca (por ejemplo, un aumento en el tamaño de la malla) entonces si éste ha tenido un efecto significativo sobre la población podrían determinarse dos regresiones diferentes de la c.p.u.e. en función del esfuerzo para los períodos anterior y posterior al cambio.

10.2 Modelo de Schaefer

Otro método de análisis que depende, principalmente de datos de captura y esfuerzo, es el de SCHAEFER (1954, 1957). La biomasa de la población B, se considera como una entidad única, la cual, si no existiera la pesca, aumentaría a una tasa determinada por su volumen, es decir:

en la que la expansión f (B) es una función de B que será cero cuando B = 0, y cuando B está en su máximo nivel, B_M, y que tendrá un máximo para un valor intermedio de B.

Por consiguiente, cuando hay pesca

donde Y = captura.

Es obvio que la población permanecerá constante si Y = f (B), de manera que para cualquier volumen de la población habrá una cierta captura de equilibrio, que será máxima cuando f (B) sea máxima.

La forma de f (B) puede ser determinada a partir de los datos de captura y esfuerzo, a condición de que haya también alguna información (por ejemplo, de marcaciones) mediante la cual los valores de la captura por unidad de esfuerzo puedan convertirse en términos absolutos, es decir, si el coeficiente q (k₂ de la notación de SCHAEFER) es conocido, Así, si los valores de la captura por unidad de esfuerzo son conocidos al principio y al final de un año:

población inicial B₁ = 1/q (Y/f)₁
población final B₂ = 1/q (Y/f)₂
población media

entonces B₂ - B₁ = cambio en la población = f (B) - Y

ó

donde Y es la captura durante el año.

De ordinario, la captura por unidad de esfuerzo no se conocerá a principios del ano, sino el valor medio a lo largo de todo el año. En cambio, la captura por unidad de esfuerzo al principio del año podrá ser estimada como la media de las capturas normales por unidad de esfuerzo durante los doce meses precedentes y los doce subsiguientes. Por lo tanto, puede obtenerse un par de valores de y 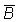para cada año, y trazando la gráfica del uno contra el otro, puede establecerse la relación entre la captura de equilibrio y el volumen de la población. El ajuste puede hacerse más rápido si se asume una cierta expresión para f (B), por ejemplo, la ecuación

f (B) = aB (B_M - B)

la cual si se representa gráficamente en función de B da una parábola. Esta forma de curva se ajusta mejor trazando en función de B, lo que da una línea recta. Este método de análisis tiene mucho en común con el de la sección precedente: ambos intentan obtener la relación de equilibrio entre la captura y el esfuerzo (o alguna de sus transformaciones) mediante un ajuste adecuado de los datos de una pesquería que está cambiando, el uno tomando en cuenta los datos de esfuerzo en años anteriores, y el otro, los cambios en la captura por unidad de esfuerzo. Este modelo tiene evidentes ventajas por su sencillez y solamente requiere pocos datos. Asimismo da la impresión de estar más estrechamente vinculado con las realidades de una población natural que el modelo analítico de la sección anterior, al menos cuando en este último no se tienen en cuenta los posibles cambios en los parámetros de crecimiento, mortalidad y reclutamiento, correlacionados con las variaciones de la abundancia de la población.

No obstante, estas ventajas son fundamentalmente superficiales. El modelo analítico puede ser modificado para tener en cuenta las complejidades de cualquier población natural mientras que el modelo de Schaefer es muy difícil de modificar. Al mismo tiempo, la tasa de incremento natural de una población no viene determinada única y simplemente por la biomasa de la población en un momento determinado. El reclutamiento viene establecido (aparte de por factores ambientales) por la población adulta existente en cierto tiempo anterior, a veces en un plazo de varios años. El incremento de la biomasa de la población debida al crecimiento de los individuos, ya sea en términos absolutos o como porcentaje de la masa presente, depende tanto, si no más, que de la biomasa total, de la estructura por edades de la población. Con el fin de tener en cuenta estos efectos se precisa alguna forma de modelo analítico.

10.3 Cambios en la selectividad

La cuestión más simple, y quizás la más importante, en lo referente al efecto de un posible cambio en la selectividad es la de si tal cambio determinará un aumento o una disminución de la captura media. Esto se puede determinar según Allen (1953) comparando el peso de los individuos de la talla a la que se pretende liberarlos, con la probabilidad de que puedan ser capturados de nuevo y el peso medio que tengan cuando son apresados. Es decir, que si W_c = peso medio de los peces individuales cuando tienen la longitud media de selección 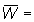peso medio de los peces existentes en la captura que pasan de W_c entonces, la captura aumentará liberando a los peces si E x W > W_c, en la que E = probabilidad de que el pez sea capturado posteriormente 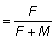si la mortalidad natural y la debida a la pesca son constantes. O bien, en función de la relación entre mortalidad por pesca y mortalidad natural, la captura aumentará si 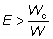. El término de la derecha de esta desigualdad podrá ser calculado fácilmente mediante observaciones sencillas de la composición de las capturas por edades.

Algunos efectos más detallados de los cambios en la selectividad pueden determinarse también a partir de un conocimiento de la composición por tallas de las capturas (véase GULLAND, 1961, 1964). Así, inmediatamente después de un cambio en el arte no habrá cambios en la población, y el número de peces de un tamaño determinado l, capturados con el nuevo arte (por ejemplo, con un tamaño de malla mayor) vendrá dado por:

(10,1)

donde

₁N₁ = número desembarcado por el arte antiguo.
₁N_k = número desembarcado por el nuevo arte.
₁r₁ = proporción retenida por el arte antiguo.
₁r₂ = proporción retenida por el nuevo arte.

Si también ₁W es el peso medio de los peces de longitud l, entonces, el peso total W₁ capturado con el arte antiguo viene dado por:

(10,2)

y el peso capturado con el nuevo arte, W_k, es:

(10,3)

también definiremos

Igualmente, el número total de peces desembarcados por el arte antiguo N₁, y retenidos por el nuevo arte N_k, puede ser expresado por:

Si los pesos medios ₁W y el número de individuos correspondiente se disponen en columnas paralelas, estos cálculos de sumas de productos son fáciles de realizar en la mayoría de las máquinas calculadoras. El cambio inmediato actual en los desembarques puede ser expresado como una proporción, L, de los desembarques iniciales, donde:

Cuando tiene lugar un aumento en la longitud media de selección, los peces liberados por el nuevo arte, pero que hubieran podido ser capturados con el arte antiguo, crecerán, y después de un tiempo, alcanzarán el tamaño al cual serán retenidos por el nuevo arte, y las capturas aumentarán.

El número, N_R, de peces liberados que anteriormente habrían sido capturados, será igual a N₁ - N_k. Si se capturan ciertas cantidades de peces pequeños que se devuelven al mar, y que no son desembarcados, el número total de individuos liberados será mayor que la reducción de los mismos en las capturas y podrá calcularse con la fórmula:

(10,4)

en la que ₁N_c es el número de peces de l, longitud, capturados por el arte antiguo incluidos los devueltos al mar. De estos peces, un número 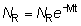sobrevivirán hasta ₂t_c, la edad media de primera captura con la nueva malla, donde t es la diferencia entre ₂t_c y la edad media de los peces liberados. A su vez, de estos peces, se capturará en definitiva un número E N_R, en que E es la tasa de explotación (F/F + M cuando las mortalidades son constantes). Puesto que todas las mortalidades, etc., para peces mayores que ₂l_c no cambian, la distribución por tamaños de esos peces será la misma que las de los N_k peces, de manera que, después de un período, las capturas con el nuevo arte aumentarán según una proporción Q, cuando:

(10,5)

De este modo, lo desembarques W₂, a la larga vendrán dados por:

W₂ = W₁ (1 - L) (1 + Q) (10,6)

Este nivel de los desembarques puede ser alcanzado solamente varios años después del cambio en la selectividad.

Tal nivel sólo se alcanzará completamente cuando haya transcurrido un período, igual a la duración de la vida del pez en la pesquería, desde el cambio de la selectividad, aunque estará próximo a tal valor en un momento bastante anterior. Las capturas en el período intermedio podrán calcularse del modo siguiente: con el fin de estimar los desembarques en el momento t', supongamos que el pez del tamaño liberado haya crecido hasta una cierta talla l'. Entonces, en un momento t' posterior al cambio del tamaño de la malla, los peces de tamaño mayor de l' habrán sido capturados por el arte antiguo cuando tenían un tamaño comprendido en el margen de selección, de modo que la población y las capturas de estos peces apenas habrán registrado variación con dicho cambio, y el peso de los peces de talla l > l' sería ₁W ₁N_R. Los peces de longitud inferior a l' habrán estado sujetos a la influencia de la nueva malla durante su vida en la fase explotada, de forma que la población y las capturas de los peces de estas tallas podría ser la misma que en el estado de equilibrio a largo plazo con la nueva malla, y el peso de los peces capturados de longitud l < l' sería (1 + Q)₁W₁N_R. El peso total capturado será W', y vendrá dado por:

es decir:

(10,7)

El método puede extenderse a poblaciones pescadas con más de un arte algunos de los cuales puede que no cambien sus selectividades. Aquí las ecuaciones (9.1) y (9.3) se aplican separadamente a cada flota, para encontrar los efectos inmediatos. El factor Q será el mismo para todas y es dado por una extensión de la ecuación (9.5) en la forma:

(10.8)

donde la sumación de N_k incluye los peces capturados por todos los artes (omitiendo los peces que son menores que la nueva longitud de selección y que son capturados por artes cuya selectividad no cambia) pero la suma de N_R incluirá solamente artes cuya selectividad cambie.

Los cálculos necesarios para evaluar los resultados de un cambio del tamaño de la malla cuando están funcionando dos artes, que posiblemente capturan peces de tamaño distinto, se exponen en la planilla de trabajo que aparece en las págs. 131-132.

10.4 Pesquerías que actúan recíprocamente

Los métodos anteriores pueden también ser usados para el estudio de la acción mutua de pesquerías diferentes en particular de una pesquería (A) dedicada principalmente a una especie determinada (por ejemplo, arenque) pero que incidentalmente captura peces jóvenes de otras especies (por ejemplo, eglefino), los cuales al alcanzar su tamaño comercial constituyen el objetivo principal de otra pesquería (B). Las operaciones necesarias serán en este caso las siguientes:

1. Calcular el número de peces capturados por la flota (A), o el número adicional que es capturado respecto al que se capturaría si suponemos que la flota (A) estaba cumpliendo con cierta regulación deseada (= N).

2. Calcular el número reducido de los que sobrevivirán hasta la edad de primera captura de la flota (B) (= N¹).

3. Comparar el número de éstos (= EN¹), que sería capturado con la captura presente C, de la flota (B). Entonces, el aumento en las capturas de la flota (B), que tendría lugar si la flota (A) dejara de pescar, es una proporción de la captura presente: EN¹/C. (El mismo resultado puede obtenerse comparando N¹ con el número de peces que se incorporan a la población explotada por la flota (B), que es C/E). (Ver C.I.E.M., 1960).

10.5 Ejercicios

1. La tabla que sigue da la captura por unidad de esfuerzo (captura en toneladas por 1.000 toneladas-horas de pesca de los arrastreros ingleses) y la captura total, en miles de toneladas, de bacalao y eglefino, en Islandia.

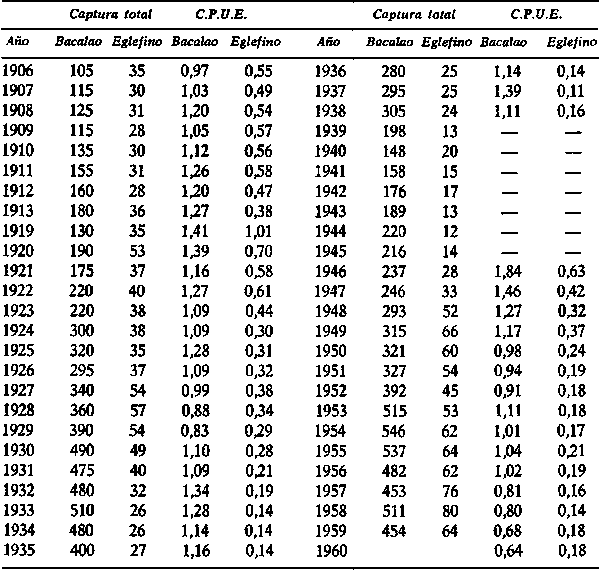
(A) Calcular el esfuerzo de pesca total, en unidades inglesas, sobre bacalao y sobre el eglefino en cada año.

(B) Si la duración media de vida en la pesquería es de dos años para el eglefino y de tres para el bacalao, relacionar la abundancia de la población con el esfuerzo de pesca pasado. ¿Hay algún indicio de que cualquiera de esas relaciones haya cambiado? En particular, examínese la curva correspondiente al eglefino para los años desde 1950 en adelante, en que se introdujo una malla mayor, y se prohibió el arrastre en ciertas zonas incluyendo algunas zonas de cría.

2. La tabla que sigue da los datos de capturas totales y capturas por unidad de esfuerzo correspondientes a las ballenas azules en el Antártico. Tomando 20.000 y 30.000 como valores alternativos del volumen de la población, correspondientes a una captura por unidad de esfuerzo de 1,00, calcúlese el cambio en el volumen de la población para cada año, y de aquí el rendimiento máximo sostenible en cada año. Represéntese esto en una gráfica frente al volumen de la población en ese año y frente al volumen cinco años antes (suponiendo que las ballenas azules se incorporan a la población explotada a los cinco años de edad). ¿Cómo pueden ser usados los datos de capturas correspondientes a los años 1939-1946?

¿Cuál es el rendimiento máximo sostenible y a qué volumen de la población es obtenido?

Año	Captura Total	C.p.u.e.
1925/26	4.697	3,30
1926/27	6.545	3,76
1927/28	8.334	4,39
1928/29	12.734	4,49
1929/30	17.898	3,13
1930/31	29.410	3,71
1931/32	6.488	4,83
1932/33	18.890	4,61
1933/34	17.349	4,76
1934/35	16.500	3,46
1935/36	17.731	3,96
1936/37	14.304	2,83
1937/38	14.923	2,00
1938/39	14.081	1,77
1939/40	11.480	-
1940/41	4.943	-
1941/42	59	-
1942/43	125	-
1943/44	339	-
1944/45	1.042	-
1945/46	3.606	1,36
1946/47	9.192	1,85
1947/48	6.908	1,12
1948/49	7.625	0,98
1949/50	6.182	0,80
1950/51	7.048	0,81
1951/52	5.130	0,63
1952/53	3.870	0,44
1953/54	2.697	0,42
1954/55	2.176	0,31
1955/56	1.614	0,37
1956/57	1.512	0,27
1957/58	1.690	0,28
1958/59	1.187	0,18
1959/60	1.228	0,14
1960/61	587*	0,105
1961/62	639*	0,093

* Omitiendo las ballenas azules pigmeas.

3. En la tabla siguiente aparecen los datos de la pesquería inglesa de eglefino en las islas Feroe, mostrando el número desembarcado en cada grupo de tallas de 5 cm., su peso medio y la proporción de cada grupo retenida por una malla de 90 mm. y una malla de 120 mm.

Talla ©	Peso medio (Gm)	Porcentaje retenido		Número desembarcado (miles)
		90 mm.	120 mm.
25-29	160	50	3	8
30-34	260	80	16	314
35-39	420	98	41	1.084
4044	630	100	72	1.409
45-49	880	100	94	1.370
50-54	1.190	100	100	952
55-59	1.570	100	100	465
60-64	1.760	100	100	255
65-69	2.530	100	100	124
70-74	3.100	100	100	73
75-79	3.800	100	100	30
80	4.600	100	100	9

a) ¿Cuál es el peso total desembarcado?

b) Si la malla actual fuese de 90 mm., ¿cuál sería la reducción de la captura (en porcentaje) que seguiría inmediatamente a su aumento a 120 mm.?

c) Si toma un promedio de seis meses para que los peces liberados crezcan hasta el tamaño de primera captura con la malla de 120 mm., ¿cuál será el efecto a largo plazo de un aumento de la malla a 120 mm., suponiendo que no hay otra pesquería, y que la mortalidad natural de los peces cuando tienen el tamaño de la selección es 0,2 y

?

d) ¿Cuál sería el efecto a largo plazo en las dos pesquerías (en porcentajes y en peso efectivo) si también hubiera una pesquería, de cordel y anzuelo, que capturara anualmente un promedio de cinco millones de peces, con un peso de 6.000 toneladas en total, y con E = 0,7? Supóngase que todos los peces capturados con anzuelo son mayores que el tamaño de selección de la malla de 120 mm.

e) ¿Cuál sería el efecto si los arrastreros devolvieran al mar el 30 % de la captura (en número), y si estos peces fuesen todos lo suficientemente pequeños para escaparse a través de una malla de 120 mm. (supóngase, por ejemplo, T = un año).

4. La captura media anual de eglefino por los arrastreros que pescaban arenque fue, en 1954-1956, la siguiente:

Tamaño	Peso capturado (toneladas)	Peso desembarcado (toneladas)	Peces (millones)
Menores de 24 cm.	2.500	-	25
24-27 cm. ... ... ...	6.000	-	45
Mayores de 27 cm.	23.500	14.000	80
TOTAL ... ... ...	32.000	14.000	150

La pesquería de eglefino desembarca un promedio de 70.000 toneladas al año de peces cuyo peso medio es 330 gr.

Si los arrastreros de arenque utilizasen una malla de tamaño mímino para la pesca demersal, ¿cuál sería el efecto en las capturas de eglefino, suponiendo que:

a) la malla legal libera todos los eglefinos menores de 24 cm.;

b) en la pesquería de eglefino se capturan alrededor de 100 millones de peces mayores de 24 cm., pero son rechazados por ser inferiores al tamaño comercial de 27 cm.;

c) los peces menores de 24 cm. que serían liberados por una malla mayor, necesitan un promedio de 6 meses para crecer hasta 24 cm. y durante este tiempo sufren una mortalidad natural de 0,2;

d) 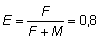(donde F, incluye todas las formas de pesca).

PLANILLA DE TRABAJO PARA EVALUAR LOS CAMBIOS EN LA SELECTIVIDAD (PARA DOS ARTES CUYAS CAPTURAS TIENEN DIFERENTE COMPISICIÓN POR TALLAS)

Parte I. Efectos inmediatos

(A)	(B)	(C)	(D)	(E)	(F)	(G)	(H)	(F)	(G)	(H)
					(F) x (1 - (E))		(F) x (E)	(F) x (1 - (E))		(F) x (E)
		Proporción retenida			Numero de individuos para el arte A			Número de individuos para el arte B
l	1W	1r1	1r2		1N1	1NR	1Nk	1N1	1NR	1Nk
					-	-	-	-	-	-
					-	-	-	-	-	-
					-	-	-	-	-	-

Parte II. Efectos a largo plazo

NR: número de individuos	NK: Número de individuos en las liberados capturas inmediatamente después del cambio
Arte A	Arte A
Arte B	Arte B
Desechado:..................	Desechado:..................
Total:..................	Total:..................

			Arte A		Arte B
E	Q	1 + Q	(1 - L)(1 + Q)	G	(1 - L)(1 + Q)	G

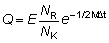
G = 1 - (1 - L)(1 + Q)